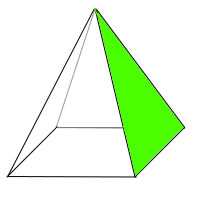
Pyramidenseitenfläche
Definition
Eine Pyramide hat immer eine Spitze und eine vieleckige Grundfläche. Von der Spitze bis zur Grundfläche gehen immer Dreiecksflächen. Jedes dieser Dreiecke ist eine Pyramidenseitenfläche. Alle diese Dreiecke bilden den => Pyramidenmantel
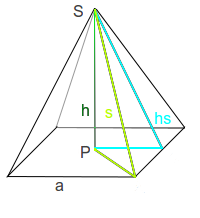Pyramidenmantelfläche
Definition
Alle Flächen zwischen der Spitze und dem Boden zusammen bilden die sogenannte Mantelfläche der Pyramide. Die einzelnen Teilflächen des Mantels sind bei einer Pyramide immer Dreiecke. Wie man die gesamte Mantelfläche M berechnet ist hier erklärt. => Ganzen Artikel lesen …
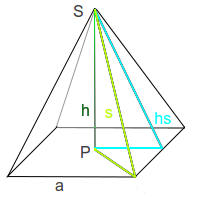Pyramidenoberfläche
A = G + A₁ + A₂ + A₃ + A₄
Alle Seitenflächen A sowie auch die Grundfläche G zusammengedacht ergeben die Oberfläche der Pyramide. Ihr Inhalt wird über die Addition aller Teilflächen berechnet. Einfach gesagt: alles was man von außen anstreichen könnte zählt zur Oberfläche der Pyramide. => Ganzen Artikel lesen …
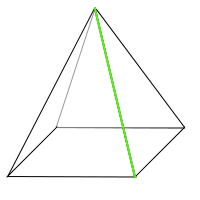Pyramidenseitenkante
Definition
Jede Kante, die von der Spitze weggeht und in einer der Ecken der Grundfläche endet ist eine Seitenkante einer Pyramide. => Ganzen Artikel lesen …
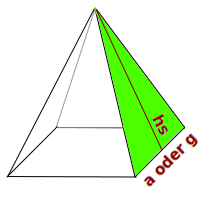Pyramidenseitenflächenhöhe
hₛ
Von der Spitze bis zur Grundfläche gehen immer Dreiecksflächen. Jedes dieser Dreiecke ist eine Pyramidenseitenfläche. Jede dieser Seitenflächen hat eine eigene Dreieckshöhe hₛ. Die Definition und Berechnung sind hier kurz erklärt. => Ganzen Artikel lesen …
A = 0,5·g·hs
Eine Pyramide hat als Seitenflächen immer nur Dreiecke. Diese Dreiecke treffen sich alle mit ihrer Spitze in der Spitze der Pyramide. Die Pyramdenseitenflächenformel gibt die Fläche von einer der mehreren dreieckigen Seitenflächen. Das ist hier kurz vorgestellt. => Ganzen Artikel lesen …
Begriffsklärung
In der Geometrie unterscheidet man bei Pyramiden die Grundfläche, verschiedene Seitenflächen, eine Mantelfläche sowie die Oberfläche (Gesamtfläche). => Ganzen Artikel lesen …
hₛ
Die Flächen die von der Pyramidenspitze bis zur Grundfläche gehen nennt man die Seitenflächen der Pyramide. Jede einzelne dieser Fälchen ist bei einer Pyramide immer ein Dreieck. Jedes dieser Dreiecke hat eine eigene Höhe. Wie man die Länge hₛ dieser Höhe der Dreiecke berechnen kann ist hier kurz erklärt. => Ganzen Artikel lesen …
