A B C D E F G H I J K L M N O P Q R S T U V W X Y Z 9 Ω
Das Banner der Rhetos-Website: zwei griechische Denker betrachten ein physikalisches Universum um sie herum.

Pyramidenmantelfläche

Definition

© 2016 - 2025


Basiswissen｜ Kurzinfo｜ Berechnung｜ Oberfläche｜ Tipps


Basiswissen


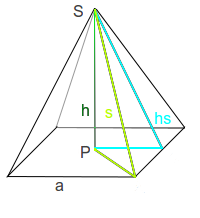
Alle Flächen zwischen der Spitze und dem Boden zusammen bilden die sogenannte Mantelfläche der Pyramide. Die einzelnen Teilflächen des Mantels sind bei einer Pyramide immer Dreiecke. Wie man die gesamte Mantelfläche M berechnet ist hier erklärt.



Bildbeschreibung und Urheberrecht
Vierseitige Pyramide als Strichbild☛


Kurzinfo


  • Die Spitze der Pyramide denkt man sich oben.
  • Die Seitenflächen sind dann immer Dreiecke.
  • Alle Seitenflächen zusammen sind die Mantelfläche M.
  • Die Grundfläche (am Boden) gehört nicht zur Mantelfläche.

Berechnung


  • Erst den Flächeninhalt aller dreieckigen Seitenflächen berechnen ...
  • diese dann zusammenaddieren gibt die Mantelfläche M.

Oberfläche


  • Mantelfläche mit der Grundfläche zusammen gibt die Oberfläche.
  • Die Oberfläche O sind alle Außenflächen der Pyramide.

Tipps