Für Figuren
Punktsymmetrie, auch Zentralsymmetrie genannt, heißt: man hat eine Figur (2D oder auch 3D) und kann für diese Figur einen Punkt finden, um den gedreht die Figur anschließend wieder genauso aussieht wie vorher. Gibt es einen solchen Punkt, ist die Figur punktsymmetrisch, anonsten nicht. => Ganzen Artikel lesen …
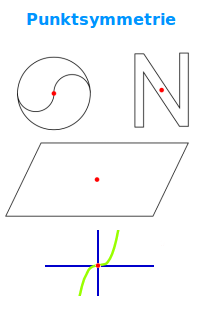Punktsymmetrie
Geometrie | Funktionsgraphen
Von Punktsymmetrie spricht man, wenn eine Figur (Geometrie, Graph) an einem Punkt gespiegelt werden kann und die Figur nach der Spiegelung wieder genauso aussieht wie vor der Spiegelung. In der Fachsprache heißt das, dass die Figur auf sich selbst abgebildet wird. => Ganzen Artikel lesen …
Übersicht
In als das Element Indium oder die Umwandlung einer Zahl oder Einheit in eine andere Art: das Wort in hat verschiedene Bedeutungen. Diese sind hier kurz vorgestellt. => Ganzen Artikel lesen …
Geometrie
Übersicht
Vierecke, Winkel, Körper: hier steht eine alphabetisch sortierte Liste zu Fachworten aus der Geometrie und eine kurze Übersicht zu wichtigen Themen der Geometrie. => Ganzen Artikel lesen …
Achsenymmetrie in der Geometrie
Definition
Achsensymmetrie gibt es für Körper (3D) und flache Figuren (2D). Wenn das Gesamtgebilde schmetterlingsartig ist, liegt Achsensymmetrie vor. Exakt: Eine Figur ist achsensymmetrisch, falls es eine Gerade g gibt, so dass es zu jedem Punkt P der Figur einen weiteren (eventuell mit P identischen) Punkt P' der Figur gibt, so dass die Verbindungsstrecke [PP'] von dieser Geraden rechtwinklig halbiert wird. Das ist hier näher erläutert. => Ganzen Artikel lesen …
Definition
Etwas nur mit Lineal und Zirkel zeichnen: konstruieren meint an sich: planvoll herstellen oder bauen. In der Geometrie meint das: nur mit Lineal und Zirkel. Das Lineal hat dabei keine Längeneinteilung. => Ganzen Artikel lesen …
Siehe auch
=> Punktsymmetrie von Graphen
