Polyeder
Geometrie
Quader, Pyramiden, Würfel: Polyeder sind geometrische Körper die als Begrenzungsflächen ausschließlich ebene Flächen haben [1]. Ebenen sind immer gerade, also nie gekrümmt. Die Grenzflächen sind damit automatisch immer auch Polygone (Vielecke). Laut Duden ist Polyeder sächlich, es heißt also: das Polyeder. Die Geometrie wird hier näher erklärt. => Ganzen Artikel lesen …
Übersicht
Als Polder bezeichnet man im Küstenschutz vollständig eingedeichte Gelände. Sie liegen oft nur knapp über dem Niveau des Meeres oder sogar darunter. Solche Polder müssen mit Pumpwerken aktiv entwässert werden. Unter anderem dazu dienten früher die vielen Windmühlen der Niederlande. Neben diesen Poldern an Küsten spricht man auch bei Flussdeichen und im Bergbau von Poldern. Das ist hier kurz vorgestellt. => Ganzen Artikel lesen …
Polyester
Material
Als Polyester bezeichnet man verschiedene Kunststoffe, sogenannte Polymerere mit Esterfunktionen. Polyester werden zum Beispiel als Faserstoffe, Flaschen, Folien oder auch als Dielektrikum für Kondensatoren eingesetzt. => Ganzen Artikel lesen …
Polymer
Chemie
Ein Polymer - wörtlich: mehrere Teile - ist ein langkettiges Molekül, zum Beispiel aus Kohlenstoff- und Sauerstoffatomen, das sich aus kürzeren Untereinheiten, den Monomeren, zusammensetzt. Das Polymer kann verzweigt sein oder auch unverzweigt. => Ganzen Artikel lesen …
… E+F-K=2, mehr unter => Eulerscher Polyedersatz
… E+F-K=2, mehr unter => Eulerscher Polyedersatz
… E+F-K=2, mehr unter => Eulerscher Polyedersatz
… E+F-K=2, mehr unter => Eulerscher Polyedersatz
… E+F-K=2, mehr unter => Eulerscher Polyedersatz
Eulerscher Polyedersatz
E+F-K = 2
Die Anzahl der Ecken plus die Anzahl der Flächen minus die Anzahl der Kanten gibt für einen Polyeder immer genau 2. Das ist der eulersche Polyedersatz. Dieser Satz gilt für alle Körper, deren Seitenflächen Vielecke (Polyeder) sind. Das ist hier ausführlicher erklärt. => Ganzen Artikel lesen …
… z. B. Dreiecke, Vierecke, Fünfecke, siehe unter => Flächenformeln
… z. B. Dreiecke, Vierecke, Fünfecke, siehe unter => Flächenformeln
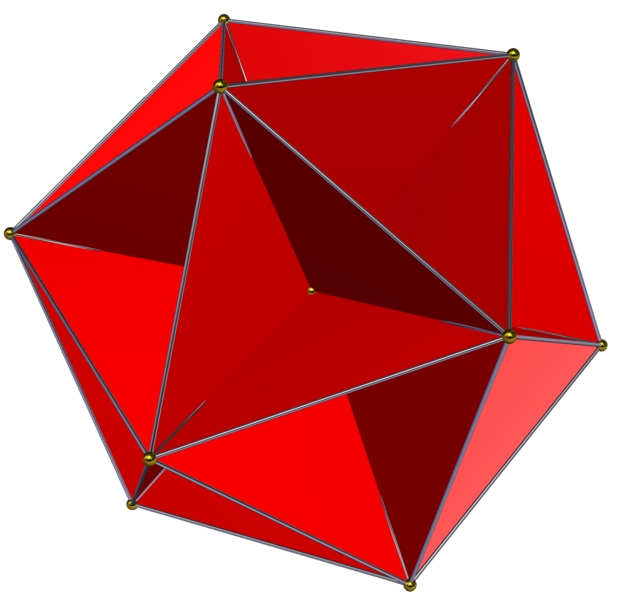Konkaves Polyeder
Vertiefungen
Ein konkaves Polyeder ist ein Körper, der ausschließlich ebene Flächen als Begrenzung hat. Alle seine Kanten sind nur gerade Strecken. Konkav heißt so ein Körper, wenn es mindestens zwei Punkte auf der Oberfläche eines solchen Körpers gibt, bei der die kürzeste Verbindungsstrecke zumindest teilweise außerhalb des Körpers verläuft. Siehe auch => konkav
… E+F-K=2, mehr unter => Eulerscher Polyedersatz
Didaktik der Geometrie
In sich widersprüchliche Definition: das Wort Polyeder heißt wörtlich übersetzt Vielflächner. Das lässt offen, ob der Körper regelmäßig (regulär) ist oder nicht. Es fehlt eine begriffliche Unterscheidung regelmäßiger und unregelmäßiger Polyeder mit nur einem Wort. => Ganzen Artikel lesen …
… z. B. Dreiecke, Vierecke, Fünfecke, siehe unter => Flächenformeln
… z. B. Dreiecke, Vierecke, Fünfecke, siehe unter => Flächenformeln
… z. B. Dreiecke, Vierecke, Fünfecke, siehe unter => Flächenformeln
… z. B. Dreiecke, Vierecke, Fünfecke, siehe unter => Flächenformeln
… z. B. Dreiecke, Vierecke, Fünfecke, siehe unter => Flächenformeln
… z. B. Dreiecke, Vierecke, Fünfecke, siehe unter => Flächenformeln
Liste
Flächen, Volumen, Anzahl der Kanten, Ecken und Seiten: hier stehen Links zu weiteren Themen: => Ganzen Artikel lesen …
… E+F-K=2, mehr unter => Eulerscher Polyedersatz
… E+F-K=2, mehr unter => Eulerscher Polyedersatz
… alle Seiten gleich lang, alle Innenwinkel gleich groß => reguläres Polyeder
Kongruente Flächen
Nach dem Spektrum Lexikon der Mathematik ist ein regehnäßiges Polyeder ein Polyeder, dessen sämtliche Begrenzungsflächen zueinander kongruente regelmäßige Vielecke sind, und bei dem in jeder Ecke gleich viele Seitenflächen zusammentreffen [1]. => Ganzen Artikel lesen …
