Polstelle
Definition | Beispiele
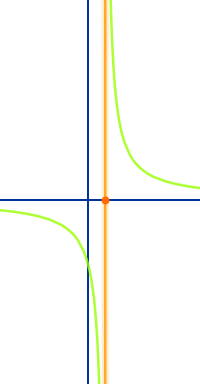
Als Polstelle bezeichnet man einen x-Wert einer Funktion, bei dem die y-Werte gegen plus oder minus unendlich gehen. Der Graph nähert sich an solchen Stellen immer mehr einer senkrechten Linie (Asymptote) an. => Ganzen Artikel lesen …
Mathematik
Polstellen von Graphen einer Funktion f(x) sind Definitionslücken an denen der Graph sich an eine senkrechte Gerade asymptotisch annähert. Hier stehen Beispiele dazu. => Ganzen Artikel lesen …
Baustelle
🏗 Ort, wo planmäßig etwas gebaut wird
Hochstelle
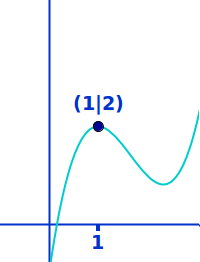
x-Wert eines Hochpunktes | Definition …
Als Hochstelle bezeichnet man den x-Wert eines Hochpunktes. Eine Hochstelle liegt damit immer auf der x-Achse. => Ganzen Artikel lesen …
Stelle
Mathematik
Man spricht von Nachkommastellen, einer Zehnerstelle oder auch Stellen von Funktionsgrpaphen. Die Fälle werden hier kurz erklärt. => Ganzen Artikel lesen …
Mathematik
Nullstelle, Baustelle, Tankstelle, Berührstelle etc.: im Zusammenhang mit einer Funktion ist eine Stelle meist eine Zahl auf der x-Achse. Hier steht eine Liste von Worten die auf Stelle enden. => Ganzen Artikel lesen …
Polstellen bestimmen
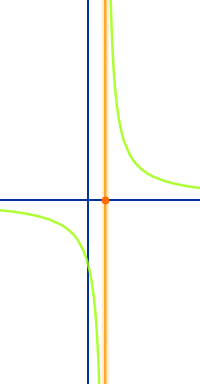
Verfahren, wie man Polstellen bestimmt
Polstellen treten normalerweise bei Funktionen auf, bei denen das x im Nenner steht. Um Polstellen zu finden, setzt man den (oder die) Nenner einer Funktionsgleichung gleich Null. Alle x-Werte, die den Nenner zu Null machen, können Polstellen sein. Wenn die Beträge der Funktionswerte in der Nähe dieser Werte dann in Richtung unendlich wachsen, dann liegt dort wirklich eine Polstelle vor. => Ganzen Artikel lesen …
… auch Unendlichkeitsstellen von Funktiosgraphen => Polstellen bestimmen
