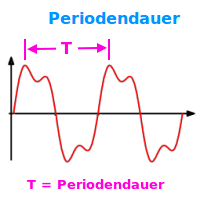
Periodendauer
Physik
Von einer Periode spricht man, wenn sich ein Vorgang öfters oder ständig wiederholt. Das Wort wird häufig im Zusammenhang mit Schwingungen und Wellen benutzt. Die übliche Abkürzung ist ein großes T. => Ganzen Artikel lesen …
Beispiele
Alle periodischen, das heißt in der Zeit wiederkehrenden Prozesse, haben eine Periodendauer. Hier stehen einige Beispiele dazu. => Ganzen Artikel lesen …
Pendeldauer
T
Ein schwingendes Pendel wiederholt immer wieder denselben Bewegungsablauf. Die Pendeldauer T ist die Zeit in Sekunden, die zwischen dem Beginn einer solche Bewegung und dem Beginn der darauffolgenden Bewegung vergeht. => Ganzen Artikel lesen …
… gerechnete Beispiele unter => Fadenpendelperiodendauern
… im Sinn der Physik => Periodendauer (Welle)
… Definition und Formel unter => Pendelgesetz
Formel
Für ein echtes Balkenpendel gilt: T = 4/3 mal pi mal der Wurzel aus l/g. Das ist hier kurz mit Legende dargelegt. => Ganzen Artikel lesen …
Theorie
Von 0 Metern bis zur Grenze des Weltraum in 100 km Höhe: mit Hilfe der Formel für ein idealisiertes Fadenpendel [1] wurden Periodendauen für verschiedene Pendellängen berechnet und hier in einer Liste zusammengestellt. => Ganzen Artikel lesen …
… ω=2πf oder ω=2π:T, mehr unter => Kreisfrequenz berechnen
… ω=2πf oder ω=2π:T, mehr unter => Kreisfrequenz berechnen
… Formel mit Erklärung unter => Pendelgesetz
.png "Eine mexikanische Welle: jedes einzelne Männchen bewegt sich ständig auf und ab und hebt und senkt dabei auch die Arme. Diese Bewegung setzt sich von rechts nach links langsam fort und gibt so eine Welle. Die Periodendauer der Welle als Ganzes ist dabei die Zeit, die ein Männchen für eine vollstände Auf-Ab-Bewegung braucht.")
Periodendauer (Welle)
Definition
Die Periodendauer T einer Welle ist identisch mit der Periodendauer T eines schwingenden Oszillators dieser Welle. Der Oszillator, bei einer Wasserwelle etwa eines der beteiligten Wassermoleküle, wird dabei als mehr oder minder ortsfest gedacht. Diese Definition ist hier kurz erläutert. => Ganzen Artikel lesen …
… Definition unter => Periode bei Sinusfunktion
… Definition unter => Periode bei Sinusfunktion
… ω=2πf oder ω=2π:T, mehr unter => Kreisfrequenz berechnen
… Definition unter => Periode bei Sinusfunktion
Dauer einen vollständigen Schwingung in einem LC-Schwingkreis
Eine bestimmte elektrische Verbindung von einer Spule und einem Kondensator nennt man einen elektrischen Schwingkreis. In solch einem Schwingkreis fließt der Strom immer wieder auf die gleiche Weise hin und her. Wie lange der Strom für eine ganze Schwingungsperiode braucht, das nennt man die Schwingkreisperiodendauer oder oft kurz nur die Periodendauer. Berechnet wird sie über die sogenannte Thomson-Formel. => Ganzen Artikel lesen …
… Definition unter => Periode bei Sinusfunktion
… Definition unter => Periode bei Sinusfunktion
Formel
Lässt man ein Stangenpendel frei hin und her pendeln, dann meint die Periodendauer die Zeit, die das Pendel für eine vollständige Hin- und Herbewegung benötigt. Gemeint ist also die Zeit, die es zum Beispiel braucht, um von ganz links über ganz rechts bis wieder hin zum Anfang ganz links zu kommen. Diese Periodendauer wird oft auch Schwingungsdauer genannt. => Ganzen Artikel lesen …
