 Parallelogramm
Parallelogramm
▰ Geometrie
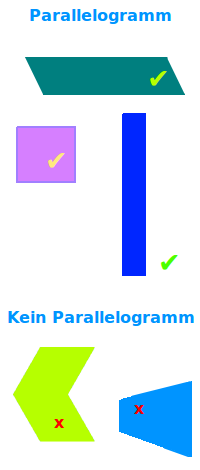
Jedes Viereck, bei dem zwei gegenüberliegende Seiten immer auch parallel zueinander sind heißt Parallelogramm oder als Fremdwort Rhomboid. Das Parallelogramm ist hier kurz vorgestellt. => Ganzen Artikel lesen …
… heißt in der Mathematik => Parallelogramm
schreibe es so: Parallelogramm…
Geometrie
Parallelogrammprisma oder Parallelepiped: diese beiden Körper haben Parallelogramme als Begrenzungsflächen und passen am ehesten auf die Idee eines 3D-Parallelogramms. Beide sind hier kurz vorgestellt. => Ganzen Artikel lesen …
… von einer Ecke zur anderen, mehr unter => Parallelogrammdiagonale
… von einer Ecke zur anderen, mehr unter => Parallelogrammdiagonale
… von einer Ecke zur anderen, mehr unter => Parallelogrammdiagonale
… von einer Ecke zur anderen, mehr unter => Parallelogrammdiagonale
… von einer Ecke zur anderen, mehr unter => Parallelogrammdiagonale
… von einer Ecke zur anderen, mehr unter => Parallelogrammdiagonale
… von einer Ecke zur anderen, mehr unter => Parallelogrammdiagonale
… Formel für den Flächeninhalt eines Parallelogramms => Parallelogrammfläche
… Formel für den Flächeninhalt eines Parallelogramms => Parallelogrammfläche
… A=a·h - Formel für die => Parallelogrammfläche
…. Formel für den Flächeninhalt eines Parallelogramms => Parallelogrammfläche
… Formel für den Flächeninhalt eines Parallelogramms => Parallelogrammfläche
… von einer Ecke zur anderen, mehr unter => Parallelogrammhöhe
… von einer Ecke zur anderen, mehr unter => Parallelogrammhöhe
… von einer Ecke zur anderen, mehr unter => Parallelogrammhöhe
… von einer Ecke zur anderen, mehr unter => Parallelogrammhöhe
… von einer Ecke zur anderen, mehr unter => Parallelogrammhöhe
… von einer Ecke zur anderen, mehr unter => Parallelogrammhöhe
… von einer Ecke zur anderen, mehr unter => Parallelogrammhöhe
Beispiele
Ein Parallelogramm ist immer ein Viereck und damit eine flache 2D-Figur. Sind gegenüberliegende Seiten immer parallel zueinander, dann liegt eindeutig ein Parallelogramm vor. Ansonsten nicht. => Ganzen Artikel lesen …
Physik
Bereits Isaac Newton (1642 bis 1727) hat beschrieben, wie man mit einem sogenannten Kräfteparallelogramm, auch Kräftediagramm genannt [2], sowohl zwei Kräfte addieren wie auch eine gegebene Kraft zerlegen kann. [1] Das Verfahren wird auch heute noch, vor allem in der Mechanik angewandt. [3] Das ist hier kurz erklärt. => Ganzen Artikel lesen …
… heißt einfach nur => Parallelogramm
 Parallelogrammdiagonale
Parallelogrammdiagonale
Definition
Eine Diagonale geht von einer Ecke eines Vielecks gerade zu einer gegenüberliegenden Ecke. Bei einem Parallelogramm gibt es immer zwei solche Strecke. Diagonale kann hier die Strecken als auch deren Längen meinen. Lies mehr zur allgemeinen Definition unter => Diagonale
… von einer Ecke zur anderen, mehr unter => Parallelogrammdiagonale
 Parallelogrammfläche
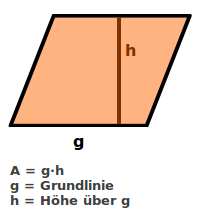
Parallelogrammfläche
Die Fläche A eines Parallelogramms
Parallelogrammfläche nennt man sowohl die Fläche des Parallelogramms als auch den Inhalt der Fläche, zum Beispiel in cm² oder m². => Ganzen Artikel lesen …
 Parallelogrammfläche berechnen
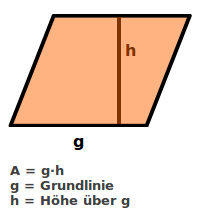
Parallelogrammfläche berechnen
Geometrie
Formel für den Flächeninhalt A eines Parallelogramms: jedes Viereck, bei dem alle gegenüberliegende Seiten immer auch parallel sind heißt Parallelogramm. Es gilt: Flächeninhalt A = g·h => Ganzen Artikel lesen …
… zum Beispiel in cm², siehe unter => Parallelogrammfläche
… z. B. in cm² oder m² => Parallelogrammfläche
… siehe unter => Parallelogrammformeln
… siehe unter => Parallelogrammfläche
 Parallelogrammhöhe
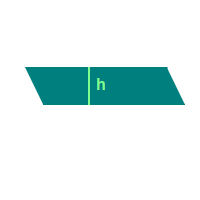
Parallelogrammhöhe
Definition
Ein Parallelogramm kann zwei verschieden große oder auch zwei gleich große Höhen haben. Eine Höhe in einem Parallelogramm steht dabei immer senkrecht auf zwei gegenüberliegenden Randstrecken des Parallelogramm. Das ist hier kurz vorgestellt. => Ganzen Artikel lesen …

