Anleitung
Man sucht eine Parabelgleichung, auch quadratische Funktion genannt, deren Graph durch zwei gegebene Punkte geht. Hier stehen eine Anleitung und Aufgaben dazu. => Ganzen Artikel lesen …
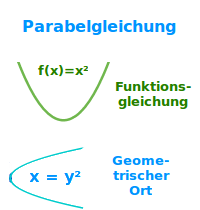Parabelgleichung
Definition
Der Graph einer quadratischen Funktion ist immer eine Parabel. Die Funktionsgleichung ist damit immer auch eine Parabelgleichung. Aber nicht jede Parabel in einem xy-Koordinatensystem kann als quadratische Funktion geschrieben werden. Das ist hier kurz erläutert. => Ganzen Artikel lesen …
Zwei
Als Zahl
Die Zwei ist die nächst natürliche Zahl nach der Eins. Das Zweifache nennt man auch das Doppelte. Als Hochzahl spricht man die Zwei auch als Quadrat aus: 3² ist 3 hoch 2 oder 3 quadrat. Hier stehen einige Besonderheiten zur Zahl Zwei. => Ganzen Artikel lesen …
Schritt-für-Schritt Anleitung
Man hat drei Punkte einer Parabel gegeben. Gesucht ist die Funktionsgleichung f(x) für die Parabel. Es werden verschiedene Lösungswege kurz vorgestellt. => Ganzen Artikel lesen …
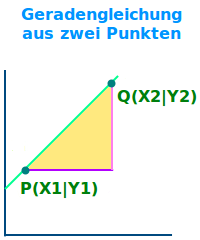Geradengleichung aus zwei Punkten
Berechnen
y= 4x+2 ist eine typische Geradengleichung. Den allgemeinen Bauplan y = m·x+b nennt man die Normalform der Geradengleichung. Man spricht auch von einer linearen Funktion. Hier wird ausführlich in Worten erklärt, wie man aus zwei gegebenen Punkten, zum Beispiel (1|6) und (3|15) die Geradengleichung aufstellt, also die Funktionsgleichung für die lineare Funktion findet. => Ganzen Artikel lesen …
… siehe unter => Parabelgleichung aus zwei Punkten
… Verfahrensbeschreibung unter => Parabelgleichung aus drei Punkten
