Parabelgleichung aus Kettenlinie
Versuch
Eine Kette ist an zwei Punkten aufgehängt und hängt dazwischen frei nach unten durch. Die Form der hängenden Kette nennt man Kettenlinie. Sie folgt in etwa (aber nicht exakt) einer Parabel. Gesucht ist eine geeignete Parabelgleichung der Form y=ax²+bx+c für Messpunkte einer real herabhängenden Kette. => Ganzen Artikel lesen …
Parabelgleichung
Definition
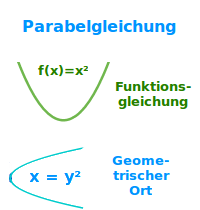
Der Graph einer quadratischen Funktion ist immer eine Parabel. Die Funktionsgleichung ist damit immer auch eine Parabelgleichung. Aber nicht jede Parabel in einem xy-Koordinatensystem kann als quadratische Funktion geschrieben werden. Das ist hier kurz erläutert. => Ganzen Artikel lesen …
Kettenlinie
Form einer frei hängenden Kette
Wenn eine Kette (oder ein Seil) an zwei Punkten festgemacht ist und dazwischen frei durchhängen kann, dann nimmt sie unter dem Einfluss einer Schwerkraft immer eine charakteristische Forme, die Kettenlinie, ein. Mathematisch wird sie über den Cosinus Hyberbolicus, kurz cosh, abgekürzt. => Ganzen Artikel lesen …
Anleitungen
Aus gegebenen Punkten, Graphen, Tabellen oder Versuchen: hier geht es zu Anleitungen, wie man daraus zu (Funktions)gleichungen kommt. => Ganzen Artikel lesen …
Parabelgleichung aus Tabelle
Anleitung
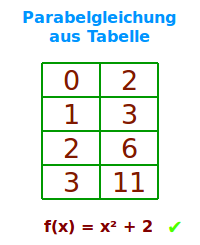
Man hat eine Tabelle mit x- und y-Wertepaaren gegeben. Gesucht ist eine Parabelgleichung, also eine quadratische Funktion, die möglichst gut auf die Wertepaare passt. Das ist hier erläutert. => Ganzen Artikel lesen …
… Übersicht unter => Parabelgleichung aufstellen
… siehe unter => Parabelgleichung aus zwei Punkten
