 Parabelast
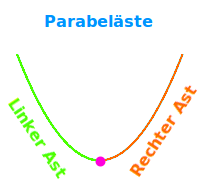
Parabelast
f(x)=x²
Ein linker und ein rechter Parabelast mit dem Scheitelpunkt in der Mitte: eine Parabel in der Geometrie oder als Funktionsgraph kann aus zwei Hälften gedacht werden. Diese zwei Hälften sind immer achsensymmetrisch zueinander. Für die Normalparabal f(x)=x² gilt: der linke Ast reicht von x = -∞ bis zum Scheitelpunkt, der rechte Ast vom Scheitelpunkt bis x = +∞. Der Scheitelpunkt selbst gehört zu keinem Ast. Die querliegende Acht ∞ ist das Zeichen für unendlich. Mehr unter => Parabeläste
 Parabeläste
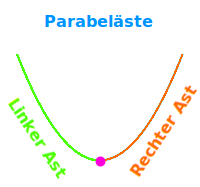
Parabeläste
Bedeutung | Beispiele
Parabeln haben immer zwei Äste: sie kommen unter anderem als Graph von quadratischen Funktionen vor. Die Parabeln stehen dann immer senkrecht in einem xy-Koordinatensystem. Das ist hier kurz erklärt. => Ganzen Artikel lesen …
Theater
In der antiken griechischen Theaterkunst war die Parabase ein eingeschalteter Teil in einer Komödie [1]. Oft vom Chor gesprochen [2] wandte sich der Dichter damit direkt an die Zuhörer. Der Inhalt der Parabase konnte auch ohne näheren Zusammenhang mit dem eigentlichen Stück sein [3]. Parabase ist auch der Titel eines Gedichtes von Johann Wolfgang von Goethe (1749 bis 1832) => Parabase (Goethe)
 Parabel
Parabel
Analysis
In der Schulmathematik ist die Parabel meist der Graph einer quadratischen Funktion, z. B. von f(x)=x²+2) [1]. Daneben gibt es aber noch weitere Bedeutungen [2], die hier auch kurz vorgestellt werden. => Ganzen Artikel lesen …
… Schnittpunkt mit x-Achse, siehe => Nullstellen von Parabeln
 Linker Parabelast
Linker Parabelast
… linke Hälfte einer Parabel, alles links vom => Scheitelpunkt
 Rechter Parabelast
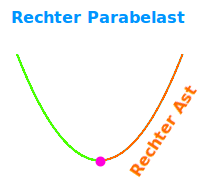
Rechter Parabelast
… die rechte Parabelhälfte, alles rechts vom => Scheitelpunkt

