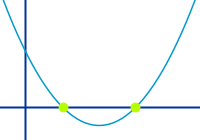
Nullstellen von Parabeln
Wo eine Parabel die x-Achse schneidet
Die x-Werte, bei denen eine Parabel die x-Achse schneidet. Kurz erklärt werden hier die Definition, Anzahlen, Beispiele und die Berechnung. => Ganzen Artikel lesen …
Nullstellen
Beispiele
Nullstellen sind x-Werte auf der x-Achse, bei denen ein Funktionsgraph die x-Achse schneidet. Hier sind Beispiele für z. B. Geraden, Parabeln, Kubische, ganzrationale und einige andere Funktionstypen. => Ganzen Artikel lesen …
Mathematik
Von x=4 bis x=7 gibt einen Bereich an. Das Wort von bezeichnet dabei den Anfang. Um eindeutig zu sagen, ob der Anfang oder auch das Ende mit dem zu dem betrachteten Bereich gehören soll, gibt es in der Mathematik speziell dafür entwickelte Schreibweisen. Siehe mehr dazu unter => Intervall
Parabeln
Übersicht
Parabeln können Graphen sein, aber auch Flugbahnen oder Formen von Brücken, Spiegeln oder anderen Dingen. Das ist hier in einer Übersicht dargestellt. => Ganzen Artikel lesen …
… Schnittpunkt mit x-Achse, siehe => Nullstellen von Parabeln
… Schnittpunkt mit x-Achse, siehe => Nullstellen von Parabeln
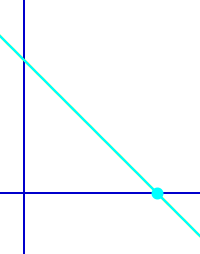Nullstellen von Geraden
Dort wo eine Gerade die x-Achse schneidet
Geraden stehen hier für den Graphen einer linearen Funktion. Eine lineare Funktion hat immer genau eine Nullstelle. Das ist der x-Wert bei dem die Gerade die x-Achse schneidet. => Ganzen Artikel lesen …
… siehe unter => Nullstellen von reinquadratischen Funktionen
… von Parabeln und quadratischen Funktionen, siehe unter => Nullstellen über ABC-Formel
Grundidee
Parabeln sind die Graphen, die zu quadratischen Funktionen gehören. Dort wo die Parabel die x-Achse schneidet liegen die sogenannten Nullstellen. Man berechnet sie mit Hilfe der pq-Formel. => Ganzen Artikel lesen …
… von Parabeln und quadratischen Funktionen, siehe unter => Nullstellen über ABC-Formel
… von Parabeln und quadratischen Funktionen, siehe unter => Nullstellen über pq-Formel
… von Parabeln und quadratischen Funktionen, siehe unter => Nullstellen über Satz des Vieta
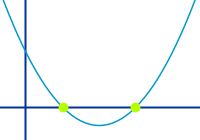Nullstellen von Parabeln bestimmen
Methoden
Parabel meint hier den Graph einer quadratischen Funktion. Die Nullstellen sind die x-Werte, bei denen die Parabel die x-Achse schneidet oder berührt. Je nachdem, wie die gegebenen Parabelgleichung aussieht, gibt es verschiedene Methoden. => Ganzen Artikel lesen …
… von Parabeln und quadratischen Funktionen, siehe unter => Nullstellen über ABC-Formel
… von Parabeln und quadratischen Funktionen, siehe unter => Nullstellen über pq-Formel
… von Parabeln und quadratischen Funktionen, siehe unter => Nullstellen über Satz des Vieta
… mit auflösen nach x, siehe unter => Nullstellen von Parabeln über umformen
… von Parabeln und quadratischen Funktionen, siehe unter => Nullstellen über ABC-Formel
… von Parabeln und quadratischen Funktionen, siehe unter => Nullstellen über pq-Formel
… von Parabeln und quadratischen Funktionen, siehe unter => Nullstellen über Satz des Vieta
… mit auflösen nach x, siehe unter => Nullstellen von Parabeln über umformen
… mit auflösen nach x, siehe unter => Nullstellen von Parabeln über umformen
… siehe unter => Nullstellen von reinquadratischen Funktionen
… von Parabeln und quadratischen Funktionen, siehe unter => Nullstellen über ABC-Formel
… siehe unter => Nullstellen von quadratischen Funktionen über Faktorisieren
… von Parabeln und quadratischen Funktionen, siehe unter => Nullstellen über pq-Formel
… von Parabeln und quadratischen Funktionen, siehe unter => Nullstellen über Satz des Vieta
Lösungsideen
f(x) = 4x² - für diese quadratische Funktion kann man ohne pq-Formel die Nullstellen berechnen, nämlich durch umformen. Das ist für Parabelgleichungen oft der einfachst Weg. Das ist hier kurz erklärt. => Ganzen Artikel lesen …
… von Parabeln und quadratischen Funktionen, siehe unter => Nullstellen über pq-Formel
… von Parabeln und quadratischen Funktionen, siehe unter => Nullstellen über Satz des Vieta
