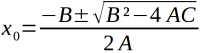Nullstellen über ABC-Formel
Berechnung
Man kann jede quadratische Gleichung in die Allgemeine Form bringen: die Allgemeine Form ist: f(x) = Ax² + Bx + C. Das A darf nicht Null sein. B und C dürfen Null sein. Damit kann man immer alle vorhandenen Nullstellen einer quadratischen Funktion berechnen. => Ganzen Artikel lesen …
Nullstellen
Beispiele
Nullstellen sind x-Werte auf der x-Achse, bei denen ein Funktionsgraph die x-Achse schneidet. Hier sind Beispiele für z. B. Geraden, Parabeln, Kubische, ganzrationale und einige andere Funktionstypen. => Ganzen Artikel lesen …
Über
Räumlich | Sinnbildlich | Kombinatorik
Von unten aus gesehen weiter oben. Im übertragenen Sinn heißt über auch so viel wie: mit Hilfe von. In der Kombinatorik steht es für einen bestimmten Term mit Fakultäten. Die Fälle sind hier kurz vorgestellt. => Ganzen Artikel lesen …
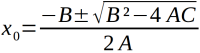ABC-Formel
Gleichungen
Mit der ABC-Formel kann man nur - aber auch jede - quadratische Gleichung lösen. Sie ist eine Alternative zur pq-Formel. => Ganzen Artikel lesen …
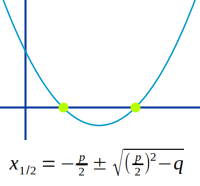Nullstellen über pq-Formel
-p/2 ± √[(p/2)²-q]
f(x) = x²-6x+8 ist eine quadratische Funktion. Das p ist hier die Zahl -6 und q ist 8. In die Formel eingesetzt erhält man die x-Werte, bei denen die Parabel die x-Achse schneidet, also die Nullstellen. Im Beispiel sind es x=2 und x=4. Das Lösungsverfahren wird hier Schritt-für-Schritt erklärt. => Ganzen Artikel lesen …
… z. B. für x-hoch-vier-Funktionen, siehe unter => Nullstellen über Substitution
… aus Funktionsterm Malkette machen => Nullstellen über Faktorisieren
… von Parabeln und quadratischen Funktionen, siehe unter => Nullstellen über ABC-Formel
