Normalverteilung
Statistik
Die meisten Werte liegen dicht beim Mittelwert, zum Rand hin Richtung extrem klein und extrem groß nimmt die Anzahl der Werte ständig ab: das mit genauen mathematischen Eigenschaften enger definiert nennt man in der Statistik eine Normalverteilung. Das ist hier näher erklärt. => Ganzen Artikel lesen …
Beispiele
Normalverteilungen, mit der klassichen Glockenkurven nach Gauß, kommen in der Technik, den Sozial- und Naturwissenschaften sehr häufig vor. Hier stehen einige Beispiele für normalverteilte Daten. => Ganzen Artikel lesen …
kann auch zusammen geschrieben werden…
Wenn du mit normalverteilt Zufallgrößen, Messwerte oder sonstige Daten meinst, auf die die Gauß-Funktion passt, dann wird normalverteilt als ein Wort geschrieben. => Ganzen Artikel lesen …
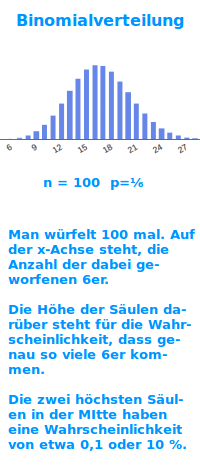Binomialverteilung
B(n,k,p)
Als Binomialverteilung bezeichnet man eine übersichtsartige Darstellung der Wahrscheinlichkeiten aller möglichen Ergebnisse einer Bernoulli-Kette: Die Verteilung gibt an, wie sich die 100 % dass irgendetwas passiert auf die einzelnen Ergebnisse verteilen, daher das Wort Verteilung. Eine Binomialverteilung kann eine Tabelle, ein Graph oder ein Histogramm sein. Das ist hier näher erklärt. => Ganzen Artikel lesen …
… so etwa wie Chi-Quadrat-Methode, Liste unter => Testen auf Normalverteilung
… für die Wahrscheinlichkeitsrechnung, siehe => Satz von Moivre-Laplace
Die Binomialverteilung einer langen Bernoulli-Kette lässt sich mathematisch näherungsweise wie eine Normalverteilung behandeln. Dies besagt der Satz von Moivre-Lapalce (siehe oben). Mit Hilfe dieses Satzes lassen sich manche Rechnungen deutlich vereinfachen.
Stochastik
Satz von Moivre-Laplace: die Binomialverteilung einer langen Bernoulli-Kette lässt sich mathematisch näherungsweise wie eine Normalverteilung behandeln. Dies besagt der Satz von Moivre-Laplace. Mit Hilfe dieses Satzes lassen sich manche Rechnungen deutlich vereinfachen. Siehe auch => Satz von Moivre-Laplace
… Größe, Masse bis zur Normalverteilung => Muschelprobe I
Statistik
Tipps zum schnellen Schätzen, ob Daten normalverteilt sind: die wenigsten Datensätze sind mathematisch perfekt normalverteilt. Man spricht üblicherweise davon, wie stark oder wie gut Daten normalverteilt sind. Das ist hier kurz erklärt. => Ganzen Artikel lesen …
Normalverteilung erkennen
Entscheiden, ob Daten in Liste normalverteilt sind
Kleinere Datenlisten (z. B. 10 Daten) können immer nur grob normalverteilt sein, da immer recht große Rundungsabweichungen auftreten. Erst bei größeren Datenmengen (z. B. 200) passen dann die Bedingungen für die Normalverteilung schon bis zur zweiten Nachkommastelle. Eine erste Überprüfung kann man mit Hilfe der Mittelwerte und der Sigmarregeln durchführen. => Ganzen Artikel lesen …
… so etwa wie Chi-Quadrat-Methode, Liste unter => Testen auf Normalverteilung
… Größe, Masse bis zur Normalverteilung => Muschelprobe I
Rohzahlen
Hier stehen einige Zahlenlisten, die mehr oder minder gut normalverteilt sind. Es ist nicht ganz einfach, künstlich solche Listen zu erzeugen. Um den Wesenskern einer Normalverteilung besser zu verstehen, ist es jedoch eine ausgezeichnet gute Lernmethode, selbst solche Zahlenfolgen zu generieren. => Ganzen Artikel lesen …
… so etwa wie Chi-Quadrat-Methode, Liste unter => Testen auf Normalverteilung
Definition
Normalverteilung mit mü=0 und sigma=1: die mathematische Funktion zur Beschreibung normalverteilter Zufallswerte heißt Gauß-Funktion (die Glockenkurve). Setzt man in diese Formel den Erwartungswerte mü=0 und die Standarabweichung sigma=1 ein, dann erhält man die sogenannte Standardnormalverteilung. => Ganzen Artikel lesen …
Beispieldaten für die Standardnormalverteil
Die folgenden Datensätze sind alle in etwa normalverteilt. Da darüberhinaus der Erwartungswert mü immer auch 0 und die Standardabweichung sigma immer gleich 1 ist, nennt man die Daten auch standardnormalverteilt: => Ganzen Artikel lesen …
… so etwa wie Chi-Quadrat-Methode, Liste unter => Testen auf Normalverteilung
Verfahren
Die Länge von Muschelschalen oder die psychologisch gemessene Introversion vieler Personen: in treten oft Messergebnisse auf, die mehr oder minder gut normalverteilt sind. Es gibt verschiedene mathematische Verfahren, um zu überprüfen, wie gut Daten normalverteilt sind. Hier steht eine kurze Übersicht dazu. => Ganzen Artikel lesen …
… so etwa wie Chi-Quadrat-Methode, Liste unter => Testen auf Normalverteilung
… so etwa wie Chi-Quadrat-Methode, Liste unter => Testen auf Normalverteilung
… so etwa wie Chi-Quadrat-Methode, Liste unter => Testen auf Normalverteilung
… siehe unter => Normalverteilung erkennen
