Normalengleichung aufstellen
Analysis
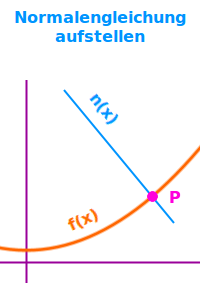
Eine Normale n(x) ist eine Gerade, die in einem bestimmten Punkt P eines anderen Graphen f(x) dort senkrecht auf dem Graphen von f(x) steht. Die Berechnung ähnelt der einer Tangentengleichung. Es gibt nur eine Stelle, an der man anders vorgeht. Das wird hier vorgestellt. => Ganzen Artikel lesen …
Mathematik
Die Gleichung einer Geraden, die senkrecht auf etwas steht: eine Normale in der Analyis ist eine Gerade, die senkrecht auf einem bestimmten Punkt eines Funktionsgraphen steht. Die Normalengleichung ist dann die Geradengleichung dazu, oft angegeben in der Form: n(x) = mx+b. Wie man sie aufstellt ist erklärt unter => Normalengleichung aufstellen
Verwendung
Das Wort „aufstellen“ wird in der Mathematik oft im Zusammenhang mit Gleichungen verwendet. Je nach Kontext gibt es verschiedene Sonderfälle. Lies zum Beispiel unter => Gleichungen aufstellen
Methoden
y=mx+b oder f(x)=ax+n: das sind häufige Darstellungen von Geradengleichungen. Eine Geradengleichung ist für die meisten Betrachtungen dasselbe wie eine lineare Funktion. Hier wird erklärt, wie man die Gleichung bestimmt, wenn bestimmte Dingen gegeben sind: Steigung und y-Achsenabschnitt, zwei Punkten, aus Graphen, Versuchen, Texten oder Ähnliches. => Ganzen Artikel lesen …
Anleitungen
Aus gegebenen Punkten, Graphen, Tabellen oder Versuchen: hier geht es zu Anleitungen, wie man daraus zu (Funktions)gleichungen kommt. => Ganzen Artikel lesen …
… siehe unter => Geradengleichung aufstellen
Sekantengleichung aufstellen
Anleitung
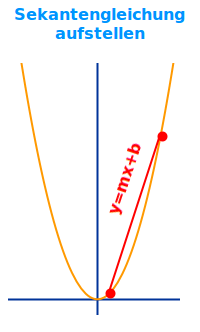
Wie man y=mx+b für eine Sekante findet: eine Sekante ist immer eine Gerade. Sie schneidet ein anderes geometrisches Gebilde in mindestens zwei verschiedenen Punkten. Kennt man zwei dieser Punkt, kann man daraus die Funktionsgleichung, die sogenannten Sekantengleichung, aufstellen. Das ist hier erklärt. => Ganzen Artikel lesen …
