 Mittelwertsatz der Integralrechnung
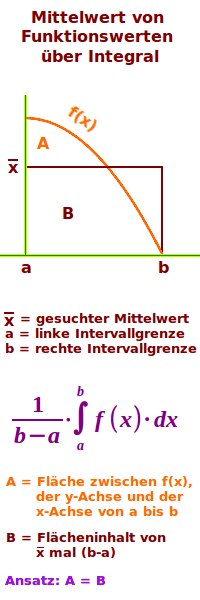
Mittelwertsatz der Integralrechnung
Definition
Arithmetisches Mittel von Funktionswerten ist gleich dem Integral dividiert durch die Breite des Intervalls. => Ganzen Artikel lesen …
Differentialrechnung
Definition des Mittelwertsatzes der Differentialrechnung: zwischen zwei beliebigen Punkten A und B einer überall differenzierbaren Funktion kann man immer eine Sekante bilden. Es gibt dann immer einen weiteren Punkt zwischen A und B, dessen Tangentensteigung gleich der Sekantensteigung von A und B ist. Das ist hier näher erklärt. => Ganzen Artikel lesen …
 Integralrechnung
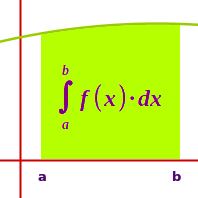
Integralrechnung
∫f(x)·dx
Zusammen mit der Differentialrechnung bildet die Integralrechnung das mathematische Teilgebiet der Analysis. Die Integralrechnung im engeren Sinn beschäftigt sich mit Flächenelementen von Graphen. In der Praxis spielt sie eine Rolle, wo die Effekte langfristig sich verändernder Prozesse aufsummiert werden. => Ganzen Artikel lesen …
… Für Intervall a bis b, siehe unter => Mittelwertsatz der Integralrechnung
F'(x) = f(x) und F(x) = F(b) - F(a)
Der Hauptsatz besteht aus zwei Teilen. Diese sind ausführlicher erklärt unter => Hauptsatz der Differential- und Integralrechnung
Analysis
Die Differentialrechnung baut auf der Idee der Ableitung auf, also der Steigung eines Graphen an einem Punkt. Kerngedanke der Integralrechnung ist die Aufleitung, veranschaulicht als Flächeninhalt von Kurven. Beide Gebiete werden zusammengefasst zur => Analysis
… Anleitung unter => Mittelwert von Funktionswerten über Integral

