3: Malkette 0

… siehe unter => Satz vom Nullprodukt

Matte

Im Sinne von Stoff, Materie in machen Worten (Dialekt) enthalten:

Eine Matte ist eine geflochtene Sitz- oder Schlafunterlage. Im Sport sind Matten schützende Bodenbedeckungen, die Stürze abmildern sollen. In Süddeutschen Dialekten steht Matte für die Speise Quark. => Ganzen Artikel lesen …

6: 0 in Malkette

… gibt immer 0, mehr unter => Satz vom Nullprodukt

7: Bruchmalkette

… z. B. (3/4)·(1/5)·(2/7)·(10/2) => Malkette aus Brüchen

8: Division von Malketten

… so etwas wie 3·4·8·7·5 durch 2 => Malkette teilen

9: Etwas zu Malkette machen

… z. B. x²-4 in (x+2)(x-2) umwandeln => Faktorisieren

10: Hoch als Malkette

… 2³ = 2·2·2 siehe unter => Potenz als Malkette

11: In Malkette umwandeln

… z. B. x²-4 in (x+2)(x-2) umwandeln => Faktorisieren

12: Klammermalkette

… wie (x+1)(2x-Siehe unter => Nachbarklammern

13: Klammermalkette auflösen

… wie (x+1)(2x-Siehe unter => Nachbarklammern auflösen

14:

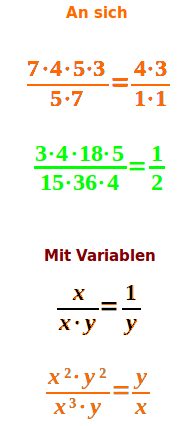Kürzen mit Malketten

… siehe unter => Malketten kürzen

15: Kürzen von Malketten

… im Zähler und Nenner, siehe unter => kürzen mit Malketten

16: Lange Malkette

… z. B. 3·4·7·8·1 oder a·b·c oder (3/4)(2/5)(1/7) => Malkette

21: Malkette aus Klammern

… wie (x+1)(2x-Siehe unter => Nachbarklammern

22: Malkette aus Klammern auflösen

… wie (x+1)(2x-Siehe unter => Nachbarklammern auflösen

23: Malkette aus Potenzen

… wie etwa 2² mal Siehe unter => Potenz mal Potenz

24: Malkette aus Zahl

… z. B. 15 als 3·5 schreiben, siehe auch => Zahl faktorisieren

25: Malkette dividieren

… so etwas wie 3·4·8·7·5 durch 2 => Malkette teilen

26: Malkette dividiert

… so etwas wie 3·4·8·7·5 durch 2 => Malkette teilen

27: Malkette durch

… so etwas wie 3·4·8·7·5 durch 2 => Malkette teilen

28: Malkette durch irgendwas geteilt

… so etwas wie 3·4·8·7·5 durch 2 => Malkette teilen

29: Malkette durch Zahl

… so etwas wie 3·4·5·6 durch 2, siehe unter => Malkette teilen

30: Malkette geteilt

… so etwas wie 3·4·8·7·5 durch 2 => Malkette teilen

31: Malkette geteilt durch irgendwas

… so etwas wie 3·4·8·7·5 durch 2 => Malkette teilen

32: Malkette gleich 0

… siehe unter => Satz vom Nullprodukt

33: Malkette gleich Null

… siehe unter => Satz vom Nullprodukt

34: Malkette gleicher Bruch

… z. B. (3/4)·(3/4)·(3/4) => Brüche potenzieren

35: Malkette gleicher Brüche

… z. B. (3/4)·(3/4)·(3/4) => Brüche potenzieren