Lok
🚅 Ein Schienenfahrzeug mit Motor, oft auch Lokomotive genannt
Lok ist eine Abkürzung von Lokomotive: auf Deutsch: die Bewegende, die Ortsverändernde. Mit Lok bezeichnet man die Zugmaschine einer Eisenbahn. Beispiele stehen unter => Loks
Silbe
Dogma, Paradoxon oder orthodox: als griechische Silbe heißen dok oder auch dox oft so viel wie: meinen, scheinen, Ruf oder Ruhm. Dazu stehen hier einige Beispiele. => Ganzen Artikel lesen …
… in der Didaktik ein Leistungskurs, siehe auch => Abi
… Abkürzung für Length overalls, meint in der Seefahrt die => Länge über alles
Loks
🚅 🚂 Beispiel(e) für Schienenfahrzeuge mit Motor
Loks - kurz für Lokomotiven - sind die Zugmaschinen für Züge im Sinne einer Eisenbahn. Die erste wirklich funktionsfähige Lok war Stephensons Rocket aus dem Jahr 1824. Die Idee zur Eisenbahn stammt aus dem Bergbau, wo man schon vorher Schienen zur Führung von Waggons benutzt hat. Hier stehen einige Beispiele für Lokomotiven. => Ganzen Artikel lesen …
🆗 meint so viel wie: alles in Ordnung, alles gut
.png "Eine historische Darstellung der Adler.")
Adler (Lok)
1835
Die erste deutsche Lokomotive: der Adler verkehrte zwischen den Städten Nürnberg und Fürth und war gebaut worden in England. => Ganzen Artikel lesen …
BRIO-Lok
Daten
Bis zu 8 cm/s Geschwindigkeit: eine kleine Spielzeug-Lok der Firma BRIO® fährt in der Lernwerkstatt Mathematik in Aachen zu Lehrzwecken. Hier stehen Daten zu der Lok. => Ganzen Artikel lesen …
Dampflok
… 🚂 Eine Lok, die mit heißem Dampf angetrieben wird, siehe auch => Lok
10 bis 20 cm/s
Auf ebenen, horizontal verlegten Schienen erreicht eine Spielzeug-Lokomotive der Marke Duplo® ohne Last eine Geschwindigkeit von gut 20 Zentimetern pro Sekunde. Bei Bergauffahrt oder mit Anhängern sowie auch schwachen Batterieständen geht die Geschwindigkeit deutlich zurück. Siehe auch => Zentimeter pro Sekunde
Duplo-Lok
Beschreibung
Duplo® ist das geschützte Warenzeichen für die große Variante von Lego®. Unter dem Namen werden auch verschiedene Spielzeuglokomotiven verkauft. Hier ist die batteriegetriebene Diesel-Lok mit techischen Daten vorgestellt. => Ganzen Artikel lesen …
… Eine E-Lok ist eine Elektrolokomotive. Sie fährt also mit Strom, siehe auch => Loks
1000 Kalorien
530 kcal, ausgesprochen als 530 Kilokalorien: das ist der Energieinhalt einer üblichen 100-Gramm-Tafel Milka-Schokolade. Ausgeschrieben sind 530000 Kalorien. Die Vorsilbe Kilo heißt immer tausend. Kilokalorie heißt als 1000 Kalorien. Das ist hier kurz vorgestellt. => Ganzen Artikel lesen …
Mal 26131938841002000
Eine Energiemenge in Kilokalorien [kcal] multipliziert mit 26131938841002000 (grob: 26 Billiarden) gibt dieselbe Energiemenge in Elektronenvolt [eV]. Eine Kilokalorie sind 1000 Kalorien. Eine Kalorie ist so viel Energie wie man zur Erwärmung von einem Gramm Wasser um 1 °C braucht. Ein Elektronenvolt ist sehr, sehr viel weniger und spielt nur bei bei der Physik submikroskopischer Prozesse eine Rolle (Atomphysik). Siehe auch => Elektronenvolt
Mal 4186,8
Der Wert in Kilokalorien multipliziert mit 4186,8 gibt denselben Energieinhalt in Joule. Dazu ein Rechenbeispiel mit einer Tafel Schokolodae von 530 Kilokalorien (kcal). => Ganzen Artikel lesen …
Mal 1000
Der Wert in Kilokalorien mal tausend (1000) gerechnet gibt denselben Energieinhalt in Kalorien ausgedrückt. Die Vorsilbe kilo heißt so viel wie tausend. Siehe auch => Kilokalorie
Mal 4,1868
Ein Wert in Kilokalorien multipliziert mit 4,1868 gibt denselben Energieinhalt in Kilojoule. Dazu ein Rechenbeispiel. => Ganzen Artikel lesen …
Linguistik
Als Kollokation bezeichnet man in der Linguistik (Sprachforschung) das gehäufte Auftreten von Wörtern in enger räumlicher oder zeitlicher Nachbarschaft. Beispiele stehen unter => Kollokationen
Beispiele
In der Linguistik ist eine Kollokation (gemeinsame Örtlichkeit) ein örtlich oder zeitlich eng zusammenliegendes Auftreten von Worten: ist ein Wort vorhanden, ist die Wahrscheinlichkeit höher, dass auch das andere Wort auftritt, als ohne das erste Wort. Mathematisch handelt es sich hier um eine bedingte Wahrscheinlichkeit. Hier stehen einige Beispiele dazu. => Ganzen Artikel lesen …
… Liste unter => Eisenbahngeschwindigkeiten
Lokal
Örtlich
Lokal, oder auch örtlich, heißt, dass etwas nur in einem begrenzten Bereich gilt und nicht überall oder in weiten Bereichen: ein Tornado beispielweise richtet oft starke Schäden an, die aber immer nur sehr lokal auftreten. => Ganzen Artikel lesen …
Definition
Lokal heißt in der Mathematik so viel wie: an einem Punkt oder Ort, nicht ausgedehnt. Eine Rate ist immer eine Änderung pro Zeit. Die lokale Änderungsrate meint damit dasselbe wie die => momentane Änderungsrate
… Definition unter => lokaler Extrempunkt
… siehe unter => Extrempunkte bestimmen
… Hochpunkte über erste Ableitung, siehe => Hochpunkte bestimmen
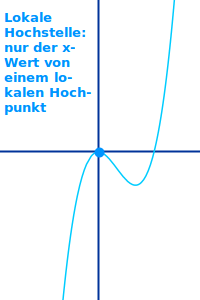Lokale Hochstelle
… der x-Wert von einem lokalen Hochpunkt, siehe unter => lokaler Hochpunkt
… Hochpunkte über erste Ableitung, siehe => Hochpunkte bestimmen
… Hochpunkte über erste Ableitung, siehe => Hochpunkte bestimmen
Definition
Eine lokale Maximalstelle ist der x-Wert von einem lokalen Maximum einer Funktion f(x). Das ist hier näher erklärt. => Ganzen Artikel lesen …
… Tiefpunkte über erste Ableitung, siehe => Tiefpunkte bestimmen
… Tiefpunkte über erste Ableitung, siehe => Tiefpunkte bestimmen
Definition
Eine lokale Minimalstelle ist der x-Wert, oder auch die entsprechende Stelle auf der x-Achse, die zu einem lokalen Tiefpunkt einer stetigen Funktion f(x) gehört. Das ist hier kurz vorgestellt. => Ganzen Artikel lesen …
… Tiefpunkte über erste Ableitung, siehe => Tiefpunkte bestimmen
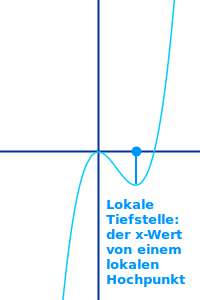Lokale Tiefstelle
… der x-Wert von einem lokalen Tiefpunkt, siehe unter => lokaler Tiefpunkt
… meint dasselbe wie => Lokales Minimum bestimmen
