 Logistische Funktion
Logistische Funktion
Wachstum
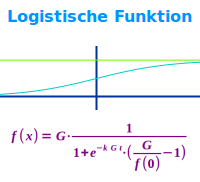
Eine Funktion der Form f(x) = G/[1+(e^(-kGx))·(G/f(0)-1)]: die logistische Funktion hat im xy-Koordinatensystem eine obere und untere Schranke (Begrenzung). Dazwischen steigt oder fällt sie kurzzeitig an. Sie verhindert den Fehler vieler exponentieller Modelle, dass das Wachstum unbebegrenzt ist. => Ganzen Artikel lesen …
 Funktion
Funktion
f(x)
f(x)=4x+8 ist eine typische mathematische Funktion: man kann für x eine beliebige Zahl einsetzen. Die Rechnung gibt dann einen y-Wert als Ergebnis der eindeutig dem eingesetzten x-Wert zugeordnet ist. Das ist die Grundidee einer Funktion. Der Gedanke wird hier ausführlich erklärt. => Ganzen Artikel lesen …
Beispiele
Zum Beispiel f(x)=1:(1+e^(-x)): als logistisch bezeichnet man eine stetige Funktion mit speziellem Bauplan deren Graph sowohl nach unten wie auch nach oben beschränkt ist und sich asymptotisch an diese Schranken annähert. Hier stehen Beispiele dazu. => Ganzen Artikel lesen …
… eine besondere Sigmoidfunktion, siehe unter => Logistische Funktion
 Quintische Funktion
Quintische Funktion
Hoch 5
Die höchste Potenz von x ist die 5: eine quintische Funktion heißt auch ganzrationale Funktion fünften Grades. Ihr Graph ist eine quintische Parabel. Die Funktion ist hier kurz vorgestellt. => Ganzen Artikel lesen …
… nähert sich x-Achse, siehe unter => f(x)=1:(1+e^x)
 Einfache logistische Funktion
Einfache logistische Funktion
f(x)=1/[1+e^(-x)]
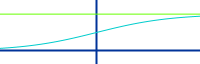
Mit typischer Sättigungskurve: die einfache oder auch elementare logistische Funktion ist die Funktion mit dem einfachstmöglichen Bauplan für einen entsprechenden Graphen. Das ist hier kurz erklärt. => Ganzen Artikel lesen …
für x-Werte von -10 bis 10 zeigt sich deutlich der „Schwanenhals“
Die logistische Funktion gehört zu den Sigmoidfunktionen. Sigmoidfunktionen haben ihren Namen von der Tatsache, dass ihre Graphen ein ein quergelegtes S (Sigma) oder einen Schwanenhals erinnern: Die Graphen nähern sich für x gegen minus unendllich einer unteren Zahl an (hier der 0) und für x gegen unendlich einer oberen Zahl (hier 1). Das kann man gut an der Wertetabelle unten erkennen. Der Wendepunkt liegt bei (0|0,5). => Ganzen Artikel lesen …
… mit Schwanenhalskurve, mehr unter => einfache logistische Funktion
… siehe unter => einfache logistische Funktion Wertetabelle

