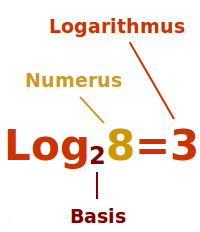
Logarithmus

Definition

2 hoch was gibt 8? Die Antwort 3 ist auch der Logarithmus. Ein Logarithmus ist eine Hochzahl, die aus einer gegebenen Basis einen gewünschten Potenzwert erzeugt. In der Zeit bevor es Rechenmaschinen gab, erleicherte der Logarithmus den Rechenaufwand erheblich. [1] Das ist hier näher erklärt. => Ganzen Artikel lesen …

6: Logarithmusgleichung mit x im Logarithmus lösen

… mehr unter => Logarithmusgleichungen mit x im Logarithmus lösen

7: Logarithmusgleichungen mit x im Logarithmuswert lösen

… mehr unter => Logarithmusgleichungen mit x im Logarithmus lösen

8: Logarithmusgleichungen mit x im Logarithmanden lösen

… mehr unter => Logarithmusgleichungen mit x im Numerus lösen

9: Logarithmusgleichung mit x im Logarithmuswert lösen

… mehr unter => Logarithmusgleichungen mit x im Logarithmus lösen