 Kugeloberfläche
Kugeloberfläche
4 mal pi mal r²
A = 4 mal pi mal Radius mal Radius: das ist die Formel für die Kugeloberfläche. Hier wird kurz erklärt, was die Kugeloberfläche ist. Mehr zur Formel steht unter => Kugeloberfläche berechnen
 Kegeloberfläche
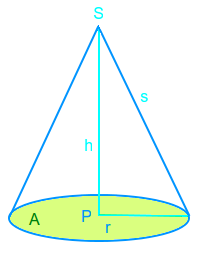
Kegeloberfläche
Formel
Die Oberfläche, genauer der Oberflächeninhalt eines Kegels meint alles, was man von außen berühren könnte: Grundfläche G und Mantelfläche M. Beides zusammen ist die Kegeloberfläche O. => Ganzen Artikel lesen …
Rechenbeispiele
Nach der Formel: A = 4/3 mal pi mal r mal r - hier stehen ein einige Rechenergebnisse sowie Beispiele aus der Astronomie. => Ganzen Artikel lesen …
 Halbkugeloberfläche
Halbkugeloberfläche
… die Hälfte der => Kugeloberfläche
Wie schnell die Oberfläche einer Kugel wächst (mit Graph)
In der Mathematik, Physik oder Chemie: kurze Erklärung von Fachworten, Symbolen und Formeln => Ganzen Artikel lesen …
 Kiste 2 Versuch Kugeloberfläche
Kiste 2 Versuch Kugeloberfläche
Anleitung
Aus Knete werden nach und nach immer größere Kugeln geformt. Dabei wird mit dem Flächenstempel die Größe der Kugeloberfläche gemessen. Sie wächst schneller als der Kugeldurchmesser. Das ist hier in einem Versuch erklärt. => Ganzen Artikel lesen …
 Kugeloberfläche berechnen
Kugeloberfläche berechnen
Kugeloberflächeninhalt, z. B. in cm²
Die Oberfläche einer Kugel, etwa in Quadratzentimetern oder Quadratkilometern ist die Grenzfläche zwischen Kugelkörper und Umgebung. Die Größe der Oberfläche nennt man auch den Kugelflächeninhalt. Es ist nur die von außen betrachtete Fläche. Hier stehen die Berechnungsformeln. => Ganzen Artikel lesen …
… zum Beispiel in cm², siehe unter => Kugeloberfläche
Herleitung
Schritt-für-Schritt Erklärung: wie berechnet man die Kugeloberfläche aus einfachsten Grundlagen? Eine Lösung bietet die Integralrechnung. => Ganzen Artikel lesen …
… Ergebnis z. B. in Quadratzentimeter, Formel unter => Kugeloberfläche
… (4/3)*Pi*r², mehr dazu unter => Kugeloberfläche
… Ein Zweieck auf einer Kugeloberfläche => Kugelzweieck

