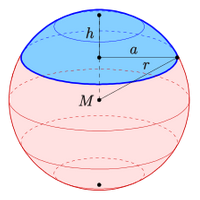
Kugelabschnitt
Anschauich
Jedes Stück, das man mit einem geraden Schnitt von einer Kugel abtrennen ist ein Kugelabschnitt (abgeschnitten!). Ein anderes Wort, also ein Synonym ist Kugelsegment. Für einen Kugelabschnitt kann man die Oberfläche und das Volumen berechnen. Das ist hier kurz vorgestelle. => Ganzen Artikel lesen …
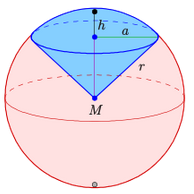Kugelausschnitt
Definition
Eine Art Kegel aus einer Kugel herausgeschnitten: aus einer Kugel wird ein kegelartiges Stück herausgeschnitten (englisch: scissors). Dieser herausgeschnittene Stück ist der Kugelsektor oder auf Deutsch auch der Kugelausschnitt. => Ganzen Artikel lesen …
Latein für Kegelschnitt
Ein Kegelschnitt ist eine Kurve, die entsteht, wenn man die Oberfläche eines Doppelkegels mit einer Ebene schneidet. Enthält die Schnittebene die Kegelspitze, so entsteht als Schnitt entweder ein Punkt oder eine Gerade oder ein sich schneidendes Geradenpaar. Ist die Spitze nicht enthalten, so entsteht eine Ellipse, eine Parabel oder eine => Hyperbel
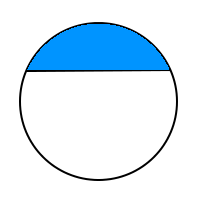Kreisabschnitt
Definition
Man hat einen Kreis und schneidet mit einem einziger geraden Schnitt ein Stück davon ab: egal wie groß es ist, ein solches Stück ist dann immer ein Kreisbaschnitt. Das Fremdwort dafür ist Kreissegment. => Ganzen Artikel lesen …
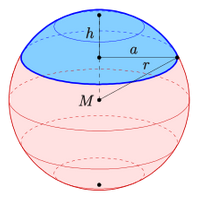Kugelabschnittsoberfläche
Definition
Pi·(2rh+a²) oder Pi·(2a²+h²) sind die Terme zur Berechnung der Oberfläche von einem Kugelabschnitt. Damit ist die gesamte Oberfläche gemeint, also die Summe aus der gewöltem Haube sowie der flachen kreisförmigen Grundfläche. Das ist hier kurz vorgestellt. => Ganzen Artikel lesen …
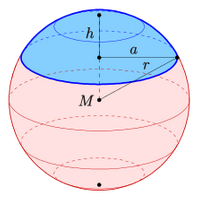Kugelabschnittsvolumen
Formel
Man nimmt eine Kugel und schneidet mit einem einzigen geraden Messerschnitt ein Stück davon ab. Das entstehende Stück heißt Kugelaschnitt. Hier steht die Formel für das Volumen. => Ganzen Artikel lesen …
Definition
Man nimmt gedanklich eine Kugel und schneidet mit einem einzigen geraden Messerabschnitt ein Stück von der Kugel ab. Ein solches Stück heißt auch Kugelabschnitt. Das ist hier näher erklärt. => Ganzen Artikel lesen …
