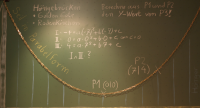Kettenlinie
Form einer frei hängenden Kette
Wenn eine Kette (oder ein Seil) an zwei Punkten festgemacht ist und dazwischen frei durchhängen kann, dann nimmt sie unter dem Einfluss einer Schwerkraft immer eine charakteristische Forme, die Kettenlinie, ein. Mathematisch wird sie über den Cosinus Hyberbolicus, kurz cosh, abgekürzt. => Ganzen Artikel lesen …
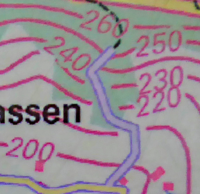Höhenlinie
Übersicht
In der Geometrie ist die Höhenlinie eine Linie, die den höchsten Punkt einer Figur auf dem kürzesten Weg mit dem Boden verbindet. In der Geodäsie (Erdvermessung) ist eine Höhenlinie fast das Gegenteil davon: eine Linie die überall dieselbe Höhe über dem Boden hat. Beides ist hier kurz erklärt. => Ganzen Artikel lesen …
Kettenglied
… ein in sich starres aber mit den Nachbargliedern bewegliches Teil einer => Kette
… sind in sich starr aber untereinander beweglich zueinander, siehe unter => Kettenglied
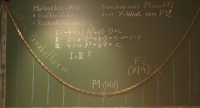Kettenlinienversuch
Lernwerkstatt
Eine frei durchhängende Kette ergibt in etwa - nicht exakt - eine Parabel. Die exakte Form heißt Kettenlinie. Dazu ist hier kurz ein Versuch vorgestellt. => Ganzen Artikel lesen …
Analysis
Freie Ketten und Seile ähneln Parabeln: wenn eine Kette (oder ein Seil) an zwei Punkten festgemacht ist und dazwischen frei durchhängen kann, dann entsteht eine Form, die einer Parabel sehr nahe kommt. Im Jahr 1669 wurde allerdings nachgewiesen, dass eine Parabel nicht ganz genau passt. Ganz genau wäre eine als Cosinus Hyperbolicus bezeichnete Funktion. Siehe auch => Kettenlinie als Parabel bestimmen
… was das meint und wie es geht unter => Parabelgleichung aus Kettenlinie
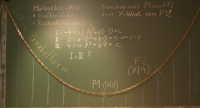Parabelgleichung aus Kettenlinie
Versuch
Eine Kette ist an zwei Punkten aufgehängt und hängt dazwischen frei nach unten durch. Die Form der hängenden Kette nennt man Kettenlinie. Sie folgt in etwa (aber nicht exakt) einer Parabel. Gesucht ist eine geeignete Parabelgleichung der Form y=ax²+bx+c für Messpunkte einer real herabhängenden Kette. => Ganzen Artikel lesen …
