Für Integrale der Form ∫f(g(x))·g'(x)·dx
Gegeben ist eine Funktion, die sich als Produkt zweier anderer Funktionen denken lässt. Man könnte immer den Ansatz über Produktintegation (partiell integrieren) probieren. Ist aber die eine Funktion die Ableitung der anderen, führt die Substitution oft schneller und mit weniger Mühe zum Ziel. Der Ansatz führt auch oft weiter, wenn ein Teil der Funktion abgeleitet einen anderen Teil der Funktion ergibt. => Ganzen Artikel lesen …
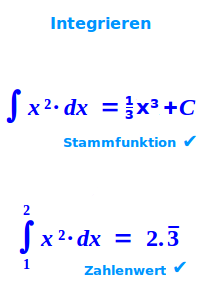Integrieren
Mathematik
Zu f(x) eine Aufleitung F(x) oder den konkreten Zahlenwert für bestimmte Grenzen dafür berechnen: beides wird oft integrieren oder auch aufleiten genannt. Hier steht eine kurze Unterscheidung der zwei Begriffe. => Ganzen Artikel lesen …
Über
Räumlich | Sinnbildlich | Kombinatorik
Von unten aus gesehen weiter oben. Im übertragenen Sinn heißt über auch so viel wie: mit Hilfe von. In der Kombinatorik steht es für einen bestimmten Term mit Fakultäten. Die Fälle sind hier kurz vorgestellt. => Ganzen Artikel lesen …
Eine Ersetzung, die Rechnungen zunächst einfacher macht
0 = x⁴-13x²+36: eine sogenannte biquadratische Gleichung ist das klassische Beispiel für ein Substitutionserverfahren. Man löst zunächst die vereinfachte Gleichung z²-13z+36 und kommt damit am Ende auch zum Ziel. Substitutionen werden in vielen Bereichen der Mathematik verwandt. => Ganzen Artikel lesen …
… siehe unter => integrieren über Substitution
Nullstellen über Substitution
0 = 2x⁴-16x²+30
Die Gleichung oben heißt biquadratisch. Solche Gleichungen kann man immer auf die pq-Formel reduzieren und dann lösen. Sie kann zwischen 0 und 4 Lösungen haben. Hier wird das Lösungsverfahren Schritt-für-Schritt erklärt. => Ganzen Artikel lesen …
… siehe unter => integrieren über Substitution
… siehe unter => Integrieren über partielle Integration
