Mathematik
Das Aufsuchen aller möglichen Stammfunktion F(x) zu einer gegebenen Funktion f(x) nennt man Integration [1]. Beispiel: f(x)=x hat als Stammfunktion zum Beispiel F(x)=½x²+1 oder auch F(x)=½x+9 oder F(x)=½x-22. Jede Funktion F(x), die abgeleitet wieder f(x) gibt eine Stammfunktion F(x) von f(x). Mehr dazu steht im Artikel => integrieren
Schrittweise Annhäherung
In der Informatik ist eine Iteration die Wiederholung einer Schleife, idealerweise verbunden mit der immer besseren Annäherung an ein gewünschtes Ergebnis. [1] Der Begriff Iteration wird nahezu gleichbedeutend mit dem Begriff Rekursion verwendet. Beide Begriffe beziehen sich auf Näherungsverfahren. Siehe unter => Iteration oder Rekursion
Die Ansteckung mit einem Parasiten
Als Parasiten bezeichnet man ein- oder mehrzellige Organismen sowie auch Viren, die anderen Organismen zu deren Schaden und zum eigenen Nutzen befallen. Beispiele sind Würmer und Zecken. => Ganzen Artikel lesen …
Beispiele
Der Integralterm ∫x·dx hat als Integranden das x: der Integrand ist das, was Integriert wird. Der Integrand ist damit identisch mit dem Funktionsterm. Dazu stehen hier Beispiele. => Ganzen Artikel lesen …
¬ Begriffsklärung
Negieren heißt so viel wie Vereinen. Eine Negation trägt immer die Idee einer Verneinung oder der Formulierung einer Art Gegenteil in sich. Dazu hier einige Beispiele: => Ganzen Artikel lesen …
Mathematik
Man misst zu zwei Zeitpunkten die Größe eines Baumes und trägt das Ergebnis in Form von zwei Punkten in ein xy-Koordinatensystem ein. Nun kann man annehmen, dass der Baum auch zu jedem Zeitpunkt zwischen den zwei gemessenen Zeitpunkten eine Größe hatte. Vorgegebene Punkte in einem Koordinatensystem so mit einer vermuteten Linie zu verbinden, dass daraus sozuagen plausible Zwischenwerte entstehen ist die Grundidee der Interpolation. Das ist hier kurz vorgestellt. => Ganzen Artikel lesen …
Evolution
Werden Teilchen „zusammengefügt zu Einheiten einer höheren Ebene“, spricht der Evolutionsbiologe Carsten Bresch [1] von einer Integration. Die „aufgebauten Strukturen neue Ganzheiten geworden sind, die neue Eigenschaften gewonnen haben“. Bresch zufolge wiederholt sich dieser Prozess im Laufe der Evolution mehrfach und ist auch heute noch nicht zu Ende gekommen. Breschs Vision ist eine Fortsetzung der biologischen Integrationen in die Sphäre der Kultur. Das ist hier kurz vorgestellt. => Ganzen Artikel lesen …
… siehe unter => integrieren über Substitution
… siehe unter => partiell integrieren
… Erklärung mit Beispiel unter => Partiell integrieren
… siehe unter => Integrieren über partielle Integration
… siehe unter => Integrieren über partielle Integration
… meistens von a bis b, siehe unter => Integrationsintervall
Das dx in ∫f(x)·dx
∫f(x)·dx liest man als: Das Integral von f(x). Das dx ist dabei das sogenannte Differential. Anschaulich steht es für die Breite einer Säule, die man im Rahmen der Säulenmethode zur Berechnung der Fläche zwischen Graph und x-Achse verwendet. Die Bedeutung des Integrationsdifferentials ist anschaulich erklärt im Artikel zum => Integralzeichen
… oft a und b genannt, siehe unter => Integrationsgrenzen
… über Integrieren, siehe unter => Fläche unter der Kurve berechnen
… ist immer ein x-Wert, mehr dazu unter => Integrationsgrenzen
… meint wahrscheinlich dasselbe wie => Linke Integrationsgrenze
… meint wahrscheinlich dasselbe wie => Rechte Integrationsgrenze
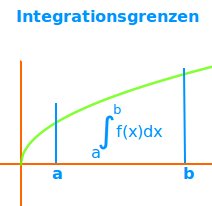Integrationsgrenzen
Definition
Die Integrationsgrenzen, auch Integrationsränder genannt, sind immer zwei x-Werte. Der linke Rand wird oft a genannt, der rechte oft b. Hier wird die anschauliche Bedeutung davon erklärt. => Ganzen Artikel lesen …
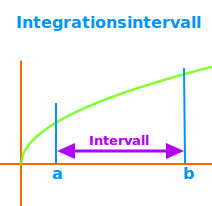Integrationsintervall
Definition
Als Integrationsintervall bezeichnet man alle x-Werte von der linken bis zur rechten Integrationsgrenze. Es ist also der Bereich der x-Achse für das man das Integral einer Funktion bestimmen möchte. Das ist hier kurz vorgestellt. => Ganzen Artikel lesen …
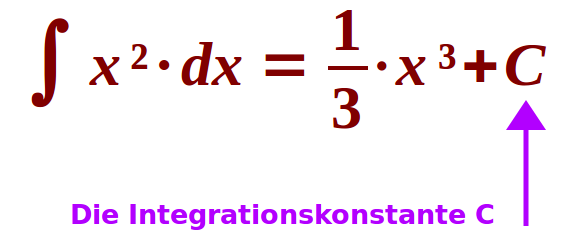Integrationskonstante
C
f(x) = 4x gibt aufgeleitet F(x) = 2x² + C. Das C am Ende ist eine reine Zahl ohne x und heißt Integrationskonstante. Diese Integrationskonstante fällt beim Ableiten von F(x) wieder weg, wird also zu 0. Das ist hier kurz erklärt. => Ganzen Artikel lesen …
… steht unter => Partiell integrieren
… oft a und b genannt, siehe => Integrationsgrenzen
… oft a und b genannt, siehe unter => Integrationsgrenzen
… meint wahrscheinlich dasselbe wie => Linke Integrationsgrenze
… meint wahrscheinlich dasselbe wie => Rechte Integrationsgrenze
… für verschiedene Funktionstypen, siehe unter => aufleiten
… das ∫, siehe unter => Integralzeichen
… Erklärung mit Beispiel unter => Partiell integrieren
… mit u und v oder g(x) und f(Siehe unter => Partielle Integration
… siehe unter => Integrieren über partielle Integration
Intellektuelle Integration
Evolution
Das rasante Anwachsen der Menschheit, die Verstädterung und verschiedene systemtheoretische Überlegungen lassen eine Degeneration, eine intellektuelle Verarmung des Menschen befürchten. Der Evolutionsbiologe Carsten Bresch sieht das anders. Er sieht in diesen Vorgängen eher Anlass, für mehr Vielfalt und Individualität. Das ist hier kurz vorgestellt. => Ganzen Artikel lesen …
Analysis
Die linke Integrationsgrenze ist eine Zahl. Sie steht für den Anfang eines Intervalls das integriert werden soll. Die linke Integrationsgrenze steht am Integralzeichen (∫) links unten. Man spricht kurz auch einfach von der linken Grenze oder dem unteren Rand. Im Zusammenhang erklärt ist die linke Integrationsgrenze im Artikel zum => Integralzeichen
… meint wahrscheinlich dasselbe wie => Linke Integrationsgrenze
