ℜ
Physik Chemie Grundschule Mathematik I Mathematik II Wissen
Kurze Worte Worte nach Alter Terme Rechner
Mathfeed Physfeed Philfeed
Das Lexikon Die Mission Die Autoren Copyright Impressum
Physik Nachhhilfe 5-10 Physik Nachhilfe 11-13 Chemie Nachhilfe 5-13 Mathe Nachhilfe 5-8 Mathe Nachhilfe 9-10 Mathe Nachhilfe 10-13
☰
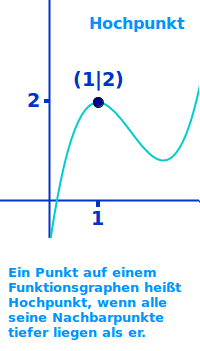
1: Hochpunkt

Analysis

Hoch- und Tiefpunkte fasst man zu den Extrempunkten zusammen: in der Schulmathematik ist ein Hochpunkt der höchste Punkt eines hügelartigen Stückes eines Graphen. Das wird hier kurz erklärt. Ergänzend wird auch die korrekte mathematische Definition gegeben. => Ganzen Artikel lesen …
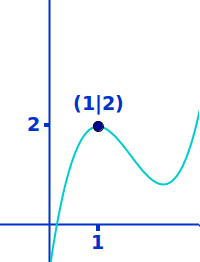
2: Hochpunkte

Analysis: Arten und Anzahlen

Es gibt lokale und absolute Hochpunkte. Bei der Unterscheidung spielt das Wort Intervall eine Rolle. Hier wird der Unterschied erklärt und es werden Beispiele gegeben. => Ganzen Artikel lesen …
3: Höhepunkt

Handlung

Die Studentenrevolten der 1960er Jahre erreichten ihren Höhenpunkt im Jahr 1968. Bilder von Gewalt waren alltäglich: ein Höhepunkt ist der dramatischste Punkt einer Handlung, bei Witzen auch die Pointe. Der höchste Punkt von Funktionsgraphen in der Mathematik heißt => Hochpunkt
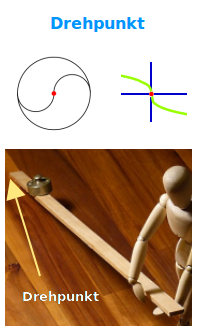
4: Drehpunkt

Geometrie | Graphen | Hebel

Ein Drehpunkt ist ein Punkt, um den anderen Dinge gedreht werden - gedanklich oder tatsächlich. In der Geometrie sowie bei punktsymmetrischen Graphen spricht man allgemein vom Symmetriezentrum. Bei Hebeln (Physik) ist das der Punkt, um den ein Hebel gedreht wird. Die Fälle werden hier kurz erklärt. => Ganzen Artikel lesen …
5: Flachpunkt

f''(x)=0

Stelle mit zweiter Ableitung gleich Null: bei einem Flachpunkt ändert sich die Steigung einer Kurve nicht. Die zweite Ableitung ist damit Null aber es liegt nicht automatisch ein Wendepunkt vor. => Ganzen Artikel lesen …
6: Absolute Hochpunkte berechnen

… über erste Ableitung und das Randverhalten, mehr unter => Absoluten Extrempunkt bestimmen
7: Absoluten Hochpunkt berechnen

… erste Ableitung und Randverhalten, mehr unter => Globalen Extrempunkt berechnen
8: Absoluten Hochpunkt bestimmen

… über f'(x) und f'(x) => Globalen Extrempunkt berechnen
9: Absoluten Hochpunkt bestimmen

Analysis

Der allerhöchste Punkt im Definitionsbereich einer Funktion oder in einem Intervall ist der sogenannte globale oder absolute Hochpunkt. Es ist also derjenige Punkt im Definitionsbereich oder einem Intervall, der den höchsten y-Wert hat. Hier steht eine Schritt-für-Schritt-Anleitung dazu. => Ganzen Artikel lesen …
10: Absoluter Hochpunkt

Funktionsgraphen

Bei Funktionsgraphen ist der absolute Hochpunkt, auch globaler Hochpunkt genannt, der höchste Punkt im gesamten Definitionsbereich. Das heißt, es gibt für die insgesamt erlaubten x-Werte keinen höheren Punkt auf dem ganzen Graphen. Mehr dazu unter => globaler Hochpunkt
11: Analytische Hochpunktbestimmung

… Anleitung steht unter => Hochpunkte über Analysis
12: Bestimmung des Hochpunktes

… z. B. über Ableitungen, siehe unter => Hochpunkte bestimmen
13: Bestimmung Hochpunkt

… z. B. über Ableitungen, siehe unter => Hochpunkte bestimmen
14: Bestimmung Hochpunkte

… z. B. über Ableitungen, siehe unter => Hochpunkte bestimmen
15: Bestimmung von Hochpunkten

… z. B. über Ableitungen, siehe unter => Hochpunkte bestimmen
16: Gegenteil eines Hochpunktes

… bei einer mathematischen Kurvendiskussion: ein => Tiefpunkt
17: Gleichung Hochpunkt Tangente

… Definition unter => Hochpunkttangente
18: Globale Hochpunkte

… Beispiele unter => globale Extrempunkte
19: Globalen Hochpunkt berechnen

Analysis

Ein globaler Hochpunkt ist der höchste Punkt in einem betrachteten Intervall. Man geht meist so vor, dass man überhaupt nach Extrempunkten sucht und dann entscheidet, wer davon ein Hoch- und wer ein Tiefpunkt ist. Das ist ausfürlich erklärt im Artikel => globalen Extrempunkt berechnen
20: Globalen Hochpunkt bestimmen

… erste Ableitung und Randverhalten, mehr unter => Globalen Extrempunkt berechnen
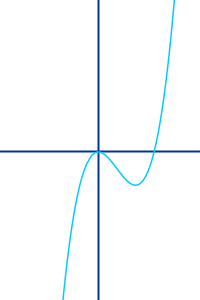
21: Globaler Hochpunkt

Analysis

Ein Punkt im Definitionsbereich einer Funktion für den es keine höheren Punkte, also keine Punkte mit größerem y-Wert gibt, nennt man einen globalen Hochpunkt. Das heißt im Umkehrschluss: alle anderen Punkte im Definitionsbereich sind niedriger. Das ist hier weiter erklärt. => Ganzen Artikel lesen …
22: Hochpunkt als Alogismus

Widersprüchliche Definitionen

Ein Hochpunkt im Sinne eines Extremums wird in der Literatur (Stand 2021) auf zwei Arten definiert: a) ein Punkt, der höher ist als alle anderen oder b) ein Punkt für den es keinen höheren gibt. => Ganzen Artikel lesen …
23: Hochpunkt analytisch bestimmen

… Anleitung steht unter => Hochpunkte über Analysis
24: Hochpunkt auffinden

… siehe unter => Hochpunkte bestimmen
25: Hochpunkt berechnen

… siehe unter => Hochpunkte bestimmen
26: Hochpunkt berechnen über Analysis

… Anleitung steht unter => Hochpunkte über Analysis
27: Hochpunkt bestimmen über Analysis

… Anleitung steht unter => Hochpunkte über Analysis
28: Hochpunkt einer Parabel

… falls Parabel nach unten geöffnet, ist das der => Scheitelpunkt einer Parabel
29: Hochpunkt einer Parabel berechnen

… ist wie Scheitelpunkt, siehe unter => Parabelhochpunkt berechnen
30: Hochpunkt einer Parabel bestimmen

… siehe unter => Parabelhochpunkt bestimmen
31: Hochpunkt finden

… Verfahren mit den ersten zwei Ableitungen => Extrempunkte bestimmen
32: Hochpunkt Tangenten

… Definition unter => Hochpunkttangente
33: Hochpunkt über Ableiten

… Anleitung steht unter => Hochpunkte über Analysis
34: Hochpunkt über Analysis

… über die erste Ableitung f'(x) => Hochpunkte über Analysis
35: Hochpunktberechnung Parabel

… ist wie Scheitelpunkt => Parabelhochpunkt berechnen
Zur Startseite von Rhetos
Startseite
Impressum
© 2010-2023


Startseite Impressum Feedback © 2010-2023