Graph einer quadratischen Funktion
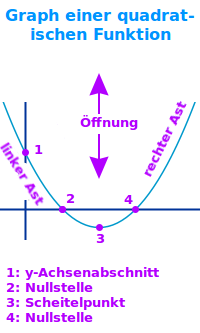
Parabel
Jede Funktion, die man so umformen kann, dass sie die Form f(x)=ax²+bx+c hat nennt man eine quadratische Funktion. Der Funktionsgraph einer solchen Funktion ist immer eine Parabel. Sie hat einige feste Eigenschaften. Diese werden hier kurz vorgestellt. => Ganzen Artikel lesen …
Graph
Bedeutungen
Funktionsgraphen, statistische Diagramme als Graphen oder reine Punktemengen in der höheren Mathematik: verschiedene Bedeutungen sind hier kurz erklärt. => Ganzen Artikel lesen …
Ganze Zahlen
Einer sind die Zahlen aus der Einerreihe: 0; 1; 2; 3; 4 und so weiter. Nicht zu den Einern zählen echte Kommazahlen wie 3,4 sowie auch Brüche deren Wert nicht ganzzahlig ist, etwa 3/4 oder 5/9. Einer dürfen aber negativ sein, wie etwa -17 oder -16. => Ganzen Artikel lesen …
Funktion
f(x)
f(x)=4x+8 ist eine typische mathematische Funktion: man kann für x eine beliebige Zahl einsetzen. Die Rechnung gibt dann einen y-Wert als Ergebnis der eindeutig dem eingesetzten x-Wert zugeordnet ist. Das ist die Grundidee einer Funktion. Der Gedanke wird hier ausführlich erklärt. => Ganzen Artikel lesen …
… ist immer 2, siehe auch => Grad einer ganzrationalen Funktion
… Graph einer Funktion mit x-hoch-4 => Parabel vierter Ordnung
… ist immer 4, siehe auch => Grad einer ganzrationalen Funktion
… siehe unter => Graph aus Parabelgleichung
