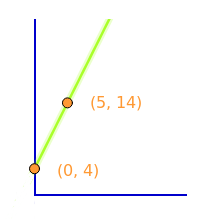
Graph aus Geradengleichung über Einsetzmethode
Beispiel
Man hat eine Geradengleichung wie zum Beispiel y=2x+4. Daraus soll ein Graph, also eine Gerade in einem xy-Koordinatensystem gezeichnet werden. Das ist hier Schritt-für-Schritt erklärt. => Ganzen Artikel lesen …
Graph
Bedeutungen
Funktionsgraphen, statistische Diagramme als Graphen oder reine Punktemengen in der höheren Mathematik: verschiedene Bedeutungen sind hier kurz erklärt. => Ganzen Artikel lesen …
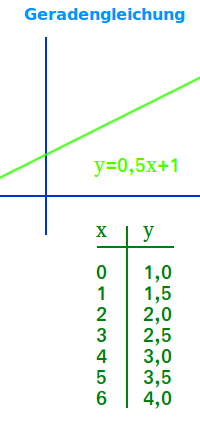Geradengleichung
Definition
y = 2x+1 ist eine typische Geradengleichung. Sie hat zwei Unbekannte, oft x und y genannt. Ihr Graph ist eine Gerade, daher der Name. Hier steht mehr zur Definition und zur Lösung solcher linearen Gleichungen. => Ganzen Artikel lesen …
Über
Räumlich | Sinnbildlich | Kombinatorik
Von unten aus gesehen weiter oben. Im übertragenen Sinn heißt über auch so viel wie: mit Hilfe von. In der Kombinatorik steht es für einen bestimmten Term mit Fakultäten. Die Fälle sind hier kurz vorgestellt. => Ganzen Artikel lesen …
… ausführliche Erklärung unter => Graph aus Geradengleichung über Einsetzmethode
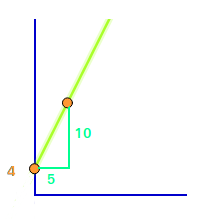Graph aus Geradengleichung
Zwei Methoden
Man hat eine Geradengleichungen in der Form y=mx+b gegegeben. Daraus soll der Graph in einem xy-Koordinatensystem gezeichnet werden. Es gibt eine Methode über einsetzen und eine über das Steigunsdreieck. Beide Methoden sind hier vorgestellt. => Ganzen Artikel lesen …
Lösen
Viele ganzrationale Gleichungen ab Grad 3 sind über feste Verfahren nur sehr aufwändig oder gar nicht lösbar. Eine Methode zum intelligenten, effizienten Probieren ist hier oft der beste Weg. Das wird hier kurz beschrieben. => Ganzen Artikel lesen …
Graph aus Geradengleichung
Anleitung
Wie man aus y=2x+4 einen Graphen zeichnet: man hat eine Geradengleichung, zum Beispiel in der Form y=mx+b. Aus jeder solchen Gleichung, auch lineare Funktion genannt, kann man einen Graphen zeichnen. Das ist hier erklärt. => Ganzen Artikel lesen …
