Physik
Als Funktechnik oder Funk bezeichnet man Techniken zum drahtlosen Senden und Empfangen von Signalen mit Hilfe sogenannter modulierter elektromagnetischer Wellen im Radiofrequenzbereich (Radiowellen) drahtlos zu übertragen. [1] => Ganzen Artikel lesen …
(Sub)Kultur
Die heutige Punk-Kultur wird erstmals in der Musikszene der 1970er greifbar Die Grundhaltung ist aggressiv, unversöhnlich, nonkonformistisch und illusionslos. Die ursprüngliche Punkszene Londons gab dem aussichtlosen Lebensgefühl von Jugendlichen einen Ausdruck. Prägend war auch der Anspruch, dass die Musik aus der Szene selbst heraus gemacht wurde, abseits des kommerziellen Konzert- und Plattengeschäfts. Der Aspekt der Trostlosigkeit und der Zurückgeworfenheit auf sich selbst lebte dann im neuen Jahrtausend unter anderem fort in der ästhetisierenden Kultur des => Cyberpunk
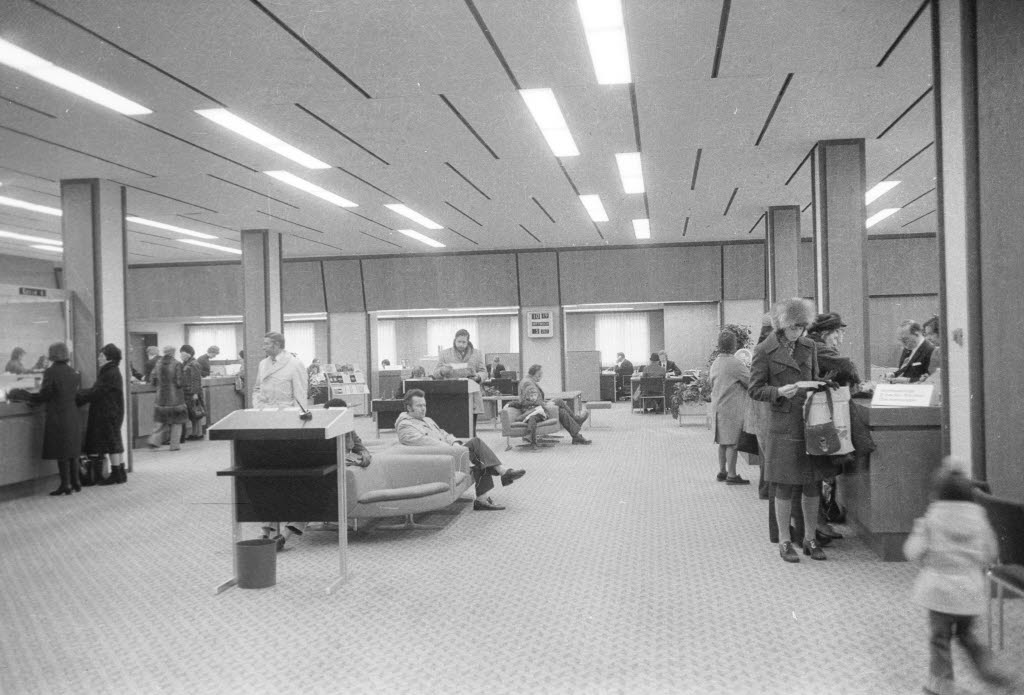 Bank
Bank
Geldwesen
Eine Bank biete gegen Bezahlung Dienstleistungen für den Zahlungs-, Kredit- und Kapitalverkehr an. Eine Bank kann Kredite vergeben, Spareinlagen verwalten oder mit Wertpapieren handeln. Ist eine Bank in allen Bereichen tätig, spricht man von einer Universalbank. Eine Bank, die selbst Geld herausgeben kann, heißt => Notenbank
Mit Hilfe von
Beispiel: Dank der pq-Formel lassen sich quadratische Gleichungen oft leicht lösen. Es gibt auch andere Methoden, diese sind aber oft schwieriger. Eine ähnliche Bedeutung wie Dank hat hier auch => mittels
Physik
Als Funken [1] oder auch Funke [5][6] bezeichnet man kleinste glühende [2] oder brennende [3] und dadurch helle Teilchen meist kurzer Lebensdauer [6]. Die Funken sind dabei oft anderen heißen oder brennenden Körper abgesprungen [4] oder elektrisch erzeugt wurden [2][3][6]. Die Farbe der Funken hängt dabei eng mit der Temperatur und weniger mit dem Material zusammen. [5] Die Funken sind dabei eine Folge der sogenannten => Stoßionisation [7]
Mathematik
Dezimalpunkt, Tausendertrennpunkt und Multiplikations-Punkt: diese drei wichtigen Bedeutungen sind hier kurz erklärt. Viele weitere Bedeutungen stehen unter => Punkte
… f(x)=0, x-Achse als Graph, mehr dazu unter => Nullfunktion
ist: 0
… Waagrechte parallel zur x-Achse, siehe unter => Einsfunktion
ist: 100x
ist: 10x
ist: 5x^2
… gibt: f'(x) = ln|x|, siehe auch => 1 durch x
ist: x
f(x)
Als 1D oder eindimensional bezeichnet man eine Funktion mit genau einer unabhängigen Variablen. Beispiel: f(x) = 2x+1. Der Graph einer solchen Funktion wird in einem 2D-Koordinatensystem dargestellt. Lies mehr unter => eindimensionale Funktion
ist: 2x
f(x,y)
Als 2D oder zweidimensional bezeichnet man eine Funktion mit zwei unabhängigen Variablen. Beispiel: f(x,y) = 2x+5y. Der Graph einer solchen Funktion wird in einem 3D-Koordinatensystem dargestellt. Lies mehr unter => zweidimensionale Funktion
ist: x^2
ist: 3x
f(w,x,y)
Als 3D oder dreidimensional bezeichnet man eine Funktion mit drei unabhängigen Variablen. Beispiel: f(w,x,y) = sin(w)-2x+5y. Der Graph einer solchen Funktion lässt sich nicht mehr anschaulich in einem Koordinatensystem darstellen. Lies mehr unter => dreidimensionale Funktion
ist: 1,5x^2
ist: 4x
ist: 2x^2
ist: 5x
ist: 2,5x^2
ist: 6x
ist: 3x^2
ist: 7x
ist: 3,5^x2
ist: 8x
ist: 4x^2
ist: 9x
ist: 4,5^x^2
…: a^x mal 1/ln(a)
… von Parabeln und quadratischen Funktionen, siehe unter => Nullstellen über ABC-Formel
f(x) = Ax² + Bx + C hat die Nullstellen [-B ± Wurzel aus (B² - 4A·C)] durch [2A]. Lies mehr dazu unter => Nullstellen über ABC-Formel

