… siehe unter => Fläche unter der Kurve
Fläche
Mathematik
Eine Fläche ist alltagssprachlich zunächst eine größere Ausdehnung ohne nennenswerte Erhebungen oder Vertiefungen. Man spricht von Eis- und Wasserflächen, von Wandflächen oder Tischflächen. Hier wird kurz erklärt, was Fläche mathematisch bedeutet und was der Unterschied zur Ebene ist. => Ganzen Artikel lesen …
Unter
Naturwissenschaften
Tiefer als etwas anderes: hält man die Hand über den Kopf, dann ist der Kopf unter der Hand: unter der Erde haben Pflanzen oft Wurzeln. Hier einige weitere Beispiele. => Ganzen Artikel lesen …
Ganze Zahlen
Einer sind die Zahlen aus der Einerreihe: 0; 1; 2; 3; 4 und so weiter. Nicht zu den Einern zählen echte Kommazahlen wie 3,4 sowie auch Brüche deren Wert nicht ganzzahlig ist, etwa 3/4 oder 5/9. Einer dürfen aber negativ sein, wie etwa -17 oder -16. => Ganzen Artikel lesen …
Bedeutungen
In der Geometrie ist eine Kurve eine zusammenhängende Linie. Sie kann gerade oder auch gebogen sein. Für Funktionen ist Kurve ein Synonym für den Graphen. Beide Bedeutungen werden hier kurz vorgestellt. => Ganzen Artikel lesen …
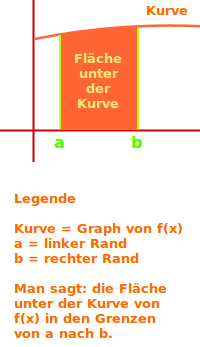
Fläche unter der Kurve
Integralrechnung
Die Fläche unter der Kurve ist die Flächen zwischen einer Kurve einer Funktion f(x), der x-Achse und - meistens - einer senkrechten Linie als linker Rand und einer senkrechten Linie als rechter Rand. Diese Definition wird hier Schritt-für-Schritt erklärt. => Ganzen Artikel lesen …
… siehe unter => Fläche unter der Kurve
… in der Integralrechnung, siehe => Fläche unter der Kurve
