Exponentialfunktion ableiten
Anleitung
Am leichtestens ist f(x)=eˣ, nicht viel schwerer ist f(x)=aˣ. Neben diesen einfachen Formen der e-Funktionen wird hier auch erklärt, wie man kompliziertere Varianten von Exponentialfunktionen ableitet, zum Beispiel f(x)=e⁽⁴ˣ⁻²⁾ oder f(x)=4⁽⁴ˣ⁻²⁾. Die Grundidee ist immer die sogenannte Kettenregel. => Ganzen Artikel lesen …
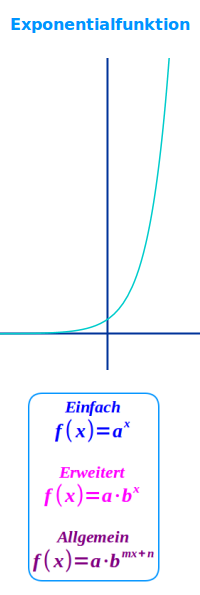
Exponentialfunktion
Funktion mit x im Exponenten
Jede Funktion, die sich umformen lässten in f(x) = a·b^T(x) heißt Exponentialfunktion. Das T(x) ist irgendein Term, bei dem eines oder mehrere x'se vorkommen. Bei einer Exponentialfunktion kommt immer ein x in einem Exponenten vor, daher auch der Name. Ist die Basis b der Potenz die Eulersche Zahl e, spricht man auch von einer e-Funktion. Das ist hier näher erklärt. => Ganzen Artikel lesen …
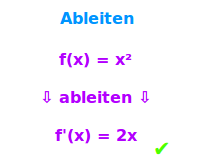
Ableiten
Verfahren
Ableiten heißt f'(x) bilden: Ableiten im engeren Sinn heißt: Für einen Funktionsgraphen an einem Punkt die Steigung bestimmen. Im allgemeineren Sinn steht es dafür, die Ableitungsfunktion f'(x) zu bestimmen. Hier sind Regeln zur Bestimmung von f'(x) zusammengestellt. => Ganzen Artikel lesen …
Zwei Fälle
f(x) = a^x ist die allgemeine und f(x) 0 e^x die spezielle e-Funktion. Für beide ist hier kurz die Aufleitung, das heißt eine Stammfunktion, angegeben. => Ganzen Artikel lesen …
Bestimmen
f(x) = a·b^x - kann auch geschrieben werden als y = a·b^x: eine solche (Funktions)gleichung kann aus Punktangaben, Texten oder sonstigen Informationen aufgestellt werden. Mehr dazu unter => Exponentialgleichung aufstellen
… siehe unter => Exponentialfunktion aufstellen
Exponentialfunktionen
Arten
Von f(x) = a^x bis zu f(x) = 400-e^(-x): hier stehen verschiedene Arten von Exponentialfunktionen mit Fachworten benannt und kurz erklärt. => Ganzen Artikel lesen …
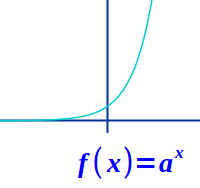
Einfache Exponentialfunktion ableiten
f(x) = a^x abgeleitet gibt f'(x) = ln(a)·a^x
Die einfache Exponentialfunktion besteht aus einer Konstanten als Basis einer Potenz und dem x als Exponent dieser Potenz. Es dürfen keine weiteren Zahlen oder Rechnungen damit verbunden sein. => Ganzen Artikel lesen …
