 Erste Ableitung
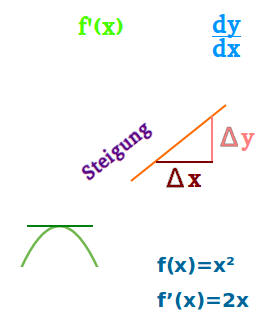
Erste Ableitung
f'(x)
Die erste Ableitung hat zwei unterschiedliche - aber zueinander passende - Bedeutungen. Es ist einmal die Ableitungsfunktion. So hat f(x)=x² die erste Ableitung f'(x)=2x. Zum anderen ist die erste Ableitung auch der Zahlenwert der Steigung für einen Punkt eines Graphen. Beide Bedeutungen werden hier gemeinsam vorgestellt. => Ganzen Artikel lesen …
Ganz am Anfang
In der Zahl 320 ist die erste Ziffer eine 3. „Die erste“ gibt hier die Position innerhalb einer Rangfolge an. Sie hat damit mathematisch gesehen die Rolle einer => Ordinalzahl
 Ableitung
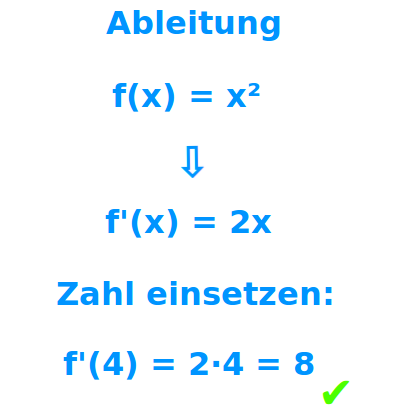
Ableitung
f'(x)
Die Ableitung steht einmal für die Steigung (als Zahl) an einem bestimmten Punkt auf einem Funktionsgraphen. Präziser spricht man hier auch vom Ableitungswert. Als Ableitung bezeichnet man auch eine Funktion f'(x), die für jeden x-Wert die dort geltende Steigung am Graphen angibt.[1][2] Präziser wäre hier: Ableitungsfunktion => Ganzen Artikel lesen …
… F(x), heißt kurz meist nur => Aufleitung
… die noch gar nicht abgeleitete Funktion, mehr unter => eigentliche Funktion
… also f'Siehe unter => dritte Ableitung
Definition
Was nach dem vierten mal ableiten einer Funktion herauskommt: die vierte Ableitung von f(x) = x⁵ ist 120x. Die vierte Ableitung => Ganzen Artikel lesen …
Beispiele
==== Beispiele ==== => Ganzen Artikel lesen …
… Bedeutungen unter => erste Ableitung gleich null
cos(x) abgeleitet gibt -sin(x)
Lernwerkstatt
Geht man bei einem einseitigen Hebel mit dem Hebelarm immer näher an den Drehpunkt, dann muss man immer mehr Kraft aufwenden, um den Hebel in einer waagrechten Lage zu halten. Der Zusammenhang zwischen dem Abstand x vom Drehpunkt und der nötigen Kraft y ist y=10:x. Anders gesagt: die Kraft y in Newton ist gleich 10 geteilt durch die Länge x des Hebelarms in Zentimetern. Dieser Artikel behandelt die anschauliche Bedeutung der ersten Ableitung y'=-10/x². => Ganzen Artikel lesen …
 Erste Ableitung als Änderungsverhältnis
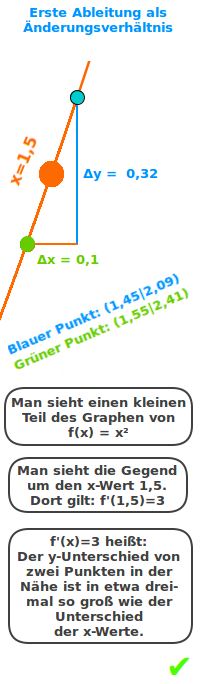
Erste Ableitung als Änderungsverhältnis
f'(x) anschaulich
Den Wert einer ersten Ableitung kann man graphisch und im Sachkontext auf verschiedene Weisen deuten. Eine Deutung ist: wie viel mal so stark ändert sich y wie x. Dazu werden hier auch praktische Versuche vorgestellt. => Ganzen Artikel lesen …
Analysis
Die erste Ableitung f'(x) einer Funktion f(x) kann man sowohl rein anschaulich nur grapisch erstellen. Zum anderen aber kann man die erste Ableitung auch anschaulich deuten, also interpretieren. Beides ist hier kurz vorgestellt. => Ganzen Artikel lesen …
… wie x² zu Siehe unter => erste Ableitung bilden
… siehe unter => Erste Ableitung bilden
… siehe unter => Erste Ableitung bilden
f'(x)
f(x) = x² ⭢ einmal ableiten gibt ⭢ f'(x) = 2x. Das f'(x) ist die erste Ableitung. Sie zu berechnen nennt man oft auch sie zu bilden. Das ist hier kurz vorgestellt. => Ganzen Artikel lesen …
… cos(x) abgeleitet gibt -sin(x), siehe auch => Ableitungsregeln
… cos(x) abgeleitet gibt -sin(x), siehe auch => Ableitungsregeln
… also von f(x)=0, steht unter => Einsfunktion ableiten
… also von f(x)=0, steht unter => Nullfunktion ableiten
… f(x)=√x ⭢ f'(x) = -½·x^(-0,5) => Wurzelfunktion ableiten
… Die => Momentangeschwindigkeit
Man hat eine Funktion s=f(t). Bildet man die erste Ableitung s'=f'(t) dann nennt man dies die Ableitung des Weges s nach der Zeit t. Diese Funktion gibt dann die Geschwindigkeit zu einem exakten Zeitpunkt t. Man spricht von der momentanen Änderungsrate oder hier präziser von der => Momentangeschwindigkeit
… wie x² zu Siehe unter => erste Ableitung bilden
… siehe unter => Erste Ableitung bilden
Begriffsklärung
Leitet man eine Funktion s=f(t) einmal ab, erhält man die Funktion für die Momentangeschwindigkeit. Leitet man die Funktion v=f(t) einmal ab, erhält man eine Funktion für die Beschleunigung. Kurz: Strecke abgeleitet nach der Zeit gibt Geschwindigkeit. Geschwindigkeit abgeleitet nach der Zeit gibt Beschleunigung. => Ganzen Artikel lesen …
… Bedeutungen unter => erste Ableitung gleich null
… Bedeutungen unter => erste Ableitung gleich null
… Bedeutungen unter => erste Ableitung gleich null
f'(x) = 0
Man hat hat eine Funktion f(x) und leitet sie einmal ab. Diese erste Ableitung nennt man auch f'(x). Diese erste Ableitung gleich null setzten heißt, man sucht einen x-Wert, bei dem für f'(x) die Zahl 0 herauskommt. Das ist hier kurz erklärt. => Ganzen Artikel lesen …
… Physik, Betriebswirtschaft etc., siehe unter => erste Ableitung im Sachzusammenhang
Praxis
Wie stark sich der Luftdruck ändert, wie schnell chemische Stoffe reagieren, wie viel extra-Gewinn eine Firma machen kann: die erste Ableitung f'(x) hat viele anschauliche Bedeutungen. Hier stehen einige Beispiele dazu. => Ganzen Artikel lesen …
… steht unter => Steigung in einem Punkt
… Bedeutungen unter => erste Ableitung gleich null
… Bedeutungen unter => erste Ableitung gleich null

