 Eigenwert
Eigenwert
… Faktor λ [2] bei Längenänderung eines Vektors, mehr unter => Eigenwert und Eigenvektor
- [1] "That value of a VARIABLE to which an OPERATION defined in that variable converges (-> CONVERGENCE). Like EQUILIBRIUM, eigen values are stable points in the domain of computation and a property of the operation. E.g., x'=(x+1)/2 converges to an eigen value of 1 (-> ITERATION)." In: Klaus Krippendorf: A Dictionary of Cybernetics. Annaberg School of Economics. University of Pennsylvania. 1986. Online: https://asc-cybernetics.org/publications/Krippendorff/A_Dictionary_of_Cybernetics.pdf
Definition
Ein Objekt oder ein Prozess wird aus einem Koordinatensystem heraus betrachtet, in dem dieses Objekt in Ruhe ist. In diesem Koordinatensystem bewegt sich das Objekt also nicht. Die Zeitdauer, die man dann an diesem Objekt für bestimmte Vorgänge misst, ist die Eigenzeit. Das Eigenzeitelement dτ (delta Tau) ist gleich dem Zeitdifferential dt der newtonschen Mechanik multipiziert mit √(1-v²/c²). Über eine Integration [2] erhält man für die Eigenzeit τ oder T₀ die Beziehung: τ = ∫√(1-v²(t')/c²) in den Grenzen von 0 bis t [2]: Lies mehr dazu unter => Zeitdilatation
 Eisenerz
Eisenerz
Geologie
Als Eisenerz bezeichnet mit Gestein mit einem relativ hohen Anteil von Eisen (Fe). Eisenerze können dabei sehr verschiedene Gesteinsarten sein. Die wichtigsten Eisenerzminerale sind Magnetit (Fe3O4, bis 72 % Eisengehalt), Hämatit (Fe2O3, bis 70 % Eisengehalt) und Siderit (FeCO3, bis 48 % Eisengehalt). => Ganzen Artikel lesen …
Jetzt
Die Vergangenheit war früher, die Gegenwart ist jetzt und die Zukunft kommt noch: Gegenwart ist der Moment oder die Zeit, in der man gerade lebt oder empfindet. Siehe auch => Zeit
… das Gewicht, das eine Waage beim Wiegen anzeigt, siehe auch => Waage
 Grenzwert
Grenzwert
Analysis
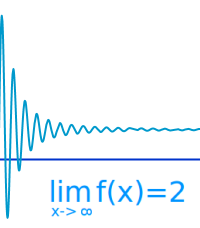
Von einem Grenzwert [1] oder Limes [7] spricht man bei Folgen, Reihen und Funktionen. Hier wird erklärt, wie der Grenzwert im Sinne der Mathematik exakt definiert ist. => Ganzen Artikel lesen …
Matrizen
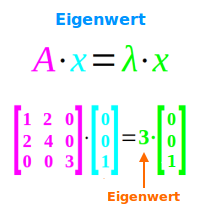
Matrix mal Vektor x = Vektor x mit neuer Länge, aber mit derselben Richtung. Die Orientierung darf eine anderere sein: „Zu einer Matrix A nennen wir v einen Eigenvektor und λ einen Eigenwert, wenn Av = λv erfüllt ist.“ [2][3] => Ganzen Artikel lesen …
Physik
Ist A eine (n × n)-Matrix, also eine quadratische Matrix, dann sind die Eigenwerte von A durch die Gleichung Ax = λx gegeben. Zur Berechnung konkreter Eigenwerte, verwendet man die Gleichung det(A − λI) = 0. [1] Siehe mehr unte => Eigenwert und Eigenvektor
Definition
Gegeben ist eine quadratische Matrix. Dazu sollen sogenannte Eigenwerte und/oder Eigenvektoren gefunden werden. Diese Aufgabenstellung nennt man das Eigenwertproblem. => Ganzen Artikel lesen …

