 Dritte Ableitung
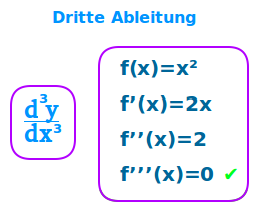
Dritte Ableitung
f'''(x)
f(x) abgeleitet gibt die erste Ableitung f'(x). Diese noch einmal abgeleitet gibt die zweite Ableitung f''(x) und das noch einmal abgeleitet gibt die dritte Ableitung f'''(x). Hier ist kurz erklärt, wie man die dritte Ableitung bildet und was sie anschaulich bedeutet. => Ganzen Artikel lesen …
 Ableitung
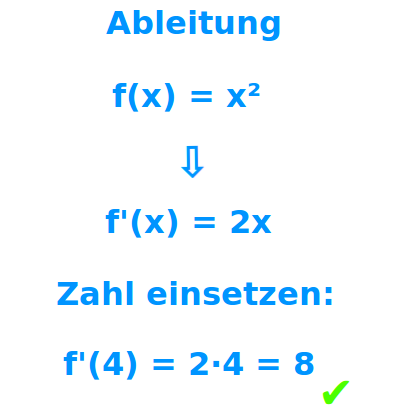
Ableitung
f'(x)
Die Ableitung steht einmal für die Steigung (als Zahl) an einem bestimmten Punkt auf einem Funktionsgraphen. Präziser spricht man hier auch vom Ableitungswert. Als Ableitung bezeichnet man auch eine Funktion f'(x), die für jeden x-Wert die dort geltende Steigung am Graphen angibt.[1][2] Präziser wäre hier: Ableitungsfunktion => Ganzen Artikel lesen …
Beispiele
f(x)=x³ einmal abgeleitet gibt f'(x)=3x². Die zweite Ableitung ist f''(x)=6x. Die dritte Ableitung ist f'''(x)=6. Hier stehen einige weitere Beispiele. Zur Bedeutung, siehe unter => Dritte Ableitung
 Erste Ableitung
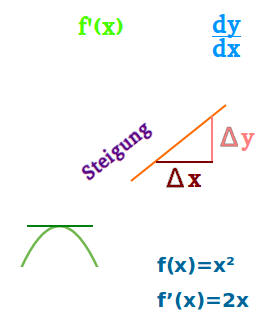
Erste Ableitung
f'(x)
Die erste Ableitung hat zwei unterschiedliche - aber zueinander passende - Bedeutungen. Es ist einmal die Ableitungsfunktion. So hat f(x)=x² die erste Ableitung f'(x)=2x. Zum anderen ist die erste Ableitung auch der Zahlenwert der Steigung für einen Punkt eines Graphen. Beide Bedeutungen werden hier gemeinsam vorgestellt. => Ganzen Artikel lesen …
… die noch gar nicht abgeleitete Funktion, mehr unter => eigentliche Funktion
… Die Drittelung von 36 gibt drei 12er, siehe auch => dritteln
… wie x³ zu 6, mehr unter => dritte Ableitung bilden
… Also f'''(x) berechnen, siehe unter => Dritte Ableitung bilden
… Also f'''(Siehe unter => Dritte Ableitung bilden
Anleitung
Man leitet eine Funktion f(x) ab, die Ableitung davon erneut und deren Ableitung wieder. Das Endergebnis ist dann die dritte Ableitung f'''(x). Ausgesprochen wird das als f-drei-Strich-von-x. Das ist hier kurz mit Beispielen vorgestellt. => Ganzen Artikel lesen …
… wie x³ zu 6, mehr unter => dritte Ableitung bilden
… Also f'''(x) bestimmen, siehe unter => Dritte Ableitung bilden
Möglichkeiten
f'''(x) = 0, also die dritte Ableitung von f(x) ist an einer Stelle null. Das eröffnet mehrere mögliche Interpretationen für den Graphen. => Ganzen Artikel lesen …
… siehe unter => Dritte Ableitung bilden
Analysis
Dritte Ableitung = 0 meint: Lage ist weiter unklar. Ansonsten kann man klar sagen, ob es ein links-rechts oder ein rechts-links Wendepunkt ist. Das ist hier mit einem Beispiel ausführlich vorgestellt. => Ganzen Artikel lesen …
… f''' als hinreichendes Kriterium, siehe unter => Wendepunkte bestimmen

