Formel
A = a·b·sin(alpha):2 - man multipliziert irgendwelche zwei Seiten a und b eines Dreiecks. Das Ergebnis multipliziert man mit dem Sinus des von a und b eingeschlossenen Winkels. Und dieses Zwischenergebnis teilt man am Ende noch durch zwei. Das Ergebnis ist dann der Flächeninhalt. Das ist hier kurz mit Legende vorgestellt. => Ganzen Artikel lesen …
 Dreiecksfläche
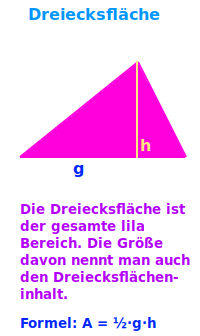
Dreiecksfläche
A=½·g·h
Die Dreiecksfläche ist die Fläche, die vom Rand des Dreiecks umschlossen wird. Will man die Größe dieser Fläche angeben kann man verschiedene Einheiten benutzen. Für sehr kleine Dreiecke eigenen sich mm² (Quadratmillimeter), für etwas größere nimmt man cm² (Quadratzentimeter, für große nimmt man m² (Quadratmeter) und für sehr große km² (Quadratkilometer). Eine übliche Abkürzung ist das große A. => Ganzen Artikel lesen …
 Über
Über
Räumlich | Sinnbildlich | Kombinatorik
Von unten aus gesehen weiter oben. Im übertragenen Sinn heißt über auch so viel wie: mit Hilfe von. In der Kombinatorik steht es für einen bestimmten Term mit Fakultäten. Die Fälle sind hier kurz vorgestellt. => Ganzen Artikel lesen …
 Sinus
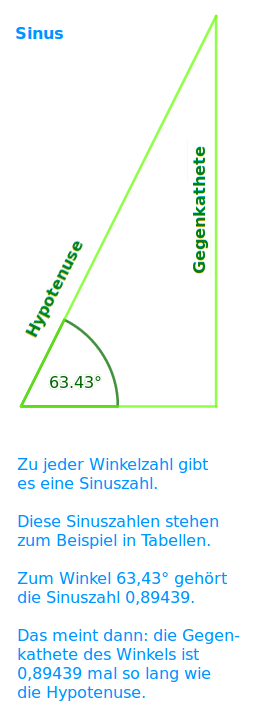
Sinus
Gegenkathete durch Hypotenuse
Der Sinus ist ein Zahl die zu einem Winkel in einem rechwinkligen Dreieck gehört. Sie sagt, wie viel mal so lang die dem Winkel gegenüberliegende Kathete ist wie die Hypotenuse. => Ganzen Artikel lesen …
… Formel unter => Dreiecksfläche über Sinus
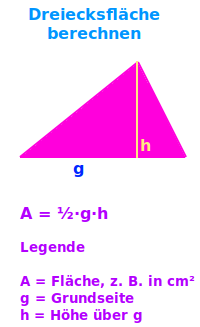 Dreiecksfläche berechnen
Dreiecksfläche berechnen
Anleitung
A = ½·g·h - das ist die einfachste Formel, um eine Dreiecksfläche zu berechnen. Diese Formel funktioniert mit jedem Dreieck. Es gibt auch andere Formeln, diese passen aber oft nur auf bestimmten Dreiecksarten. Unten steht eine Übersicht zu allen Formeln. => Ganzen Artikel lesen …
… Anleitung unter => Winkel über Sinus
… A=½·g·h ist die Grundformel für => Dreiecksfläche berechnen
… A=½·g·h ist die Grundformel für => Dreiecksfläche berechnen

