Definition
Eine Differentialgleichung ist eine Gleichung in der eine Ableitung einer gesuchten Funktion [1] und die Funktion selbst enthalten ist [2]. Die Lösung einer Differentialgleichung ist keine Zahl, sondern eine gesuchte Funktion [3] oder Menge von Funktionen [4]. => Ganzen Artikel lesen …
… z. B. y + y' = 5x => Differentialgleichung
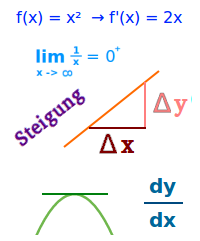Differentialrechnung
Einordnung
f'(x), Steigungen, Hoch- und Tiefpunkte: die Differentialrechnung ist ein Teilgebiet der Analysis. Die Grundidee des gesamten Themas ist die Steigung in einem Punkt. => Ganzen Artikel lesen …
Grundtyp
y = a^x ist die einfachste Form einer Exponentialgleichung. Wesentlich für eine Exponentialgleichung ist, dass die Unbekannte, hier das x, im Exponenten eines Termes vorkommt. => Ganzen Artikel lesen …
Definition
In einer „Differentialgleichung erster Ordnung ist die gesuchte Funktion y(t) ihrer ersten Ableitung ẏ(t) proportional“ [1]. Die allgemeine Form ist ẏ=C·y(t). Die allgemeine Lösung ist die Exponentialfunktion y(t) = yo·e^(C·t). Dabei sind yo und C beides je eine Konstante. Man überzeuge sich selbst, dass die erste Ableitung ẏ(t) sich nur um ein konstantes Vielfaches von y(t) unterscheidet. Siehe auch => Differentialgleichung zweiter Ordnung
Definition
In einer „Differentialgleichung zweiter Ordnung ist die gesuchte Funktion y(t) proportional zu ihrer zweiten Ableitung ÿ(t)“ [1]. Die allgemeine Form ist ÿ(t)=-C·y(t). Die allgemeine Lösung führt zu trigonometrischen Funktionen wie zum Beispiel y(t)=y₀·sin(√C·t) oder y(t)=y₀·cos(√C·t). Dabei sind y₀ und C jeweils beide konstante Werte. Man überzeuge sich selbst, dass die zweite Ableitung ÿ(t) sich nur um ein konstantes Vielfaches von y(t) unterscheidet [2]. Siehe auch => Differentialgleichung zweiter Ordnung
