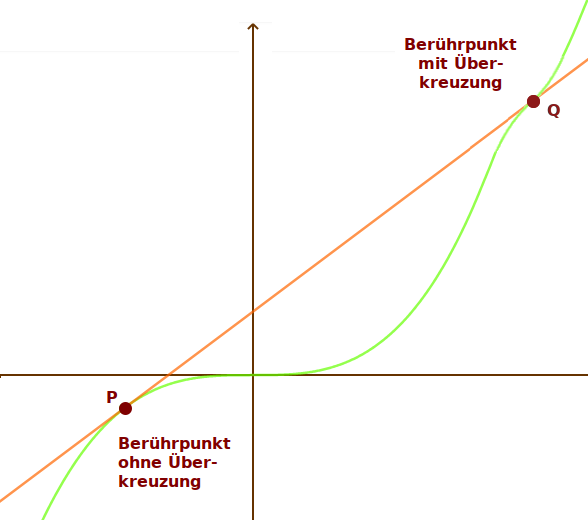
Berührpunkt
Definition
In der Geometrie ist ein Berührpunkt ein Punkt, an dem sich zwei Objekte (z. B. Kreise, Vierecke, Kugeln) nur berühren, aber nicht durchdringen: in der Analysis ist ein Berührpunkt ein Punkt von zwei Graphen, an dem beiden Graphen dieselbe Tangentensteigung haben. Dabei ist üblicherweise eine Durchdringung oder Überkreuzung erlaubt. => Ganzen Artikel lesen …
Berührpunkte
Beispiele
Die Funktion f(x) = [(x + 2) (x + 1) (x - 1) (x - 3)²] / 8 und die Funktion g(x) = 2,17x + 5,25 haben im Punkt A bei (-1,72|1,52) einen Berührpunkt. F und die x-Achse haben x=3 einen Berührpunkt. Mehr zur Definition unter => Berührpunkt
Mathematisch
Das Wort berühren wird sowohl im Zusammenhang mit Graphen als auch in der Geometrie und der Analysis (Funktionsgraphen) benutzt. Beides ist hier kurz vorgestellt. => Ganzen Artikel lesen …
… Eine Linie, die irgendetwas nur berührt, aber nicht schneidet => Tangente
… ein besonderer Schnittpunkt, siehe unter => Berührpunkt
… siehe unter => Berührpunkt
Mehrdeutigkeit durch wortentstellende Definition
Ein Berührpunkt ist mathematisch definiert als Punkt gemeinsamer Punkt zweier Graphen. Immer wenn die zwei Graphen an diesem Punkt auch dieselbe Tangentensteigung haben, ist der Punkt auch ein Berührpunkt. => Ganzen Artikel lesen …
Anleitung
Erst einen Schnittpunkt finden und dann überprüfen, ob dort die betrachteten Kurven von Funktionen dieselbe Steigung haben. Das ist hier Schritt-für-Schritt erklärt. => Ganzen Artikel lesen …
… siehe unter => Berührpunkt finden
