Arten | Beispiele
Als Ableitung f'(x) bezeichnet man im erweiterten Sinn die Ableitungsfunktion zu einer gegebenen Funktion f(x). Man unterscheidet eine erste, zweite, dritte Ableitung etc. Ableitungen werden auch nach der Art der Ausgangsfunktion f(x) unterteilt. Auf dieser Seite stehen einige Beispiele. => Ganzen Artikel lesen …
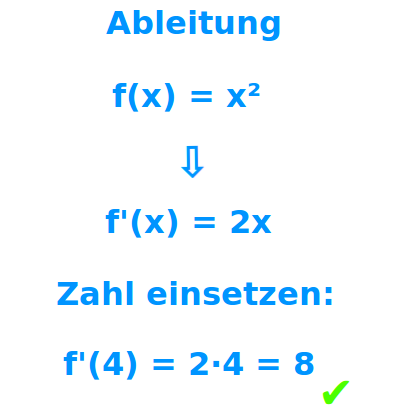Ableitung
f'(x)
Die Ableitung steht einmal für die Steigung (als Zahl) an einem bestimmten Punkt auf einem Funktionsgraphen. Präziser spricht man hier auch vom Ableitungswert. Als Ableitung bezeichnet man auch eine Funktion f'(x), die für jeden x-Wert die dort geltende Steigung am Graphen angibt.[1][2] Präziser wäre hier: Ableitungsfunktion => Ganzen Artikel lesen …
Aufleitungen
Liste für F(x)
Liste von Standardaufleitungen - Aufleitung meint hier: eine Stammfunktion F(x) einer gegebenen Funktion f(x). Aufleitungen häufig gesuchter Funktionen nennt man oft auch Stammintegrale. Hier steht eine Übersicht häufiger und wichtiger Stammintegrale. => Ganzen Artikel lesen …
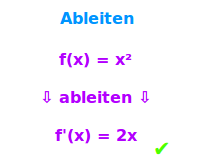Ableiten
Verfahren
Ableiten heißt f'(x) bilden: Ableiten im engeren Sinn heißt: Für einen Funktionsgraphen an einem Punkt die Steigung bestimmen. Im allgemeineren Sinn steht es dafür, die Ableitungsfunktion f'(x) zu bestimmen. Hier sind Regeln zur Bestimmung von f'(x) zusammengestellt. => Ganzen Artikel lesen …
Leistungen
🚴 Zahlenbeispiele
Sehr geringe Leistungen haben zum Beispiel Laserpointer oder eine Fernbedienung. Von mittleren Leistungen würde man bei Radfahrern sprechen. Sehr große Leistungen für menschliche Maßstäbe haben Raketen und Kraftwerke. Sie sind aber vergleichsweise klein im kosmischen Vergleich. Hier folgen nun konkrete Zahlenwerte. => Ganzen Artikel lesen …
… innen abgeleitetet mal außen abgeleitet => Ableiten über Kettenregel
… heißt => Lagrange-Notation
… ist in der Physik die => Newton-Notation
… Stelle ohne eindeutige Steigung => Nicht differenzierbar
… wie man sie schreiben kann steht unter => Notationen von Ableitungen
… wie man sie schreiben kann steht unter => Notationen von Ableitungen
… f(x) gegeben, f-Strich von (x) skizzieren => Graphisch ableiten
… Stelle ohne eindeutige Steigung => Nicht differenzierbar
Beispiele
f(x)=x³ einmal abgeleitet gibt f'(x)=3x². Die zweite Ableitung ist f''(x)=6x. Die dritte Ableitung ist f'''(x)=6. Hier stehen einige weitere Beispiele. Zur Bedeutung, siehe unter => Dritte Ableitung
… siehe unter => Formelsammlung Differentialrechnung
… heißt => Lagrange-Notation
… innere Ableitung mal äußere Ableitung, mehr unter => Ableiten über Kettenregel
… wie etwa f' oder f'', siehe unter => Notationen von Ableitungen
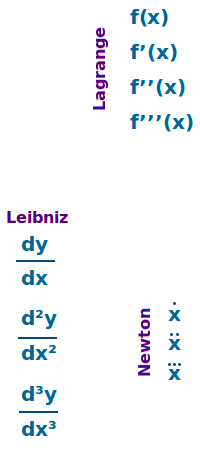Notationen von Ableitungen
Beispiele
f'(x), dy/dx oder ẋ sind drei Varianten die alle für die erste Ableitung stehen. Alle Varianten werden auch tatsächlich verwendet. Sie sind formal identisch haben aber gedanklich unterschiedliche Hintergründe. Das ist hier kurz erklärt. => Ganzen Artikel lesen …
… wie man sie schreiben kann steht unter => Notationen von Ableitungen
… siehe unter => Standardableitungen
Formelsammlung
f(x)=x² gibt abgeleitet f'(x)=2x - solche und weitere Grundbeispiele zu Ableitungsfunktionen f'(x) nennt man Standardableitungen. Hier steht eine Liste mit häufigen Standardableitungen. => Ganzen Artikel lesen …
… die noch gar nicht abgeleitete Funktion, mehr unter => eigentliche Funktion
Beispiele
==== Beispiele ==== => Ganzen Artikel lesen …
… wie man sie schreiben kann steht unter => Notationen von Ableitungen
Beispiele
f(x) = x³ einmal abgeleitet gibt f'(x) = 3x². Das dann noch einmal abgleitet gibt f''(x) = 6x¹. Dazu stehen hier noch einige Beispiele. => Ganzen Artikel lesen …
