Definition

Die Theorie des rationalen Egoismus: die Spieltheorie ist ein Teilgebiet der Mathematik. Sie beschäftigt sich mit modellhaften sozialen Situationen, in denen verschiedene Teilnehmer für sich maximale Vorteile erzielen wollen und dazu rationales Denken einsetzen.^[3]

Bildbeschreibung und Urheberrecht — Typisch für die mathematische Spieltheorie: Entscheidungskombinationen werden in Tabellen mit ausgezahlten Punkten dargestellt, oft einer Vierfeldertafel. © Christopher X Jon Jensen (CXJJensen) & Greg Riestenberg ☛

Merkmal der Spieltheorie

Charakteristisch für alle betrachteten Situationen ist, dass der Erfolg einer Entscheidung von Person davon abhängt, wie sich Person B entscheidet, aber niemand vorher die Entscheidung anderer Spielteilnehmer kennt. Dazu steht hier einige klassische Beispiele.

Beispiel: Feiglingsspiel

Zwei Personen fahren als Mutprobe in einem schnellen Auto aufeinander zu. Wer ausweicht, zeigt seine Angst und hat damit verloren. Für verschiedene Handlungsweisen gibt es verschieden viele Punkte. Lies mehr unter Feiglingsspiel ↗

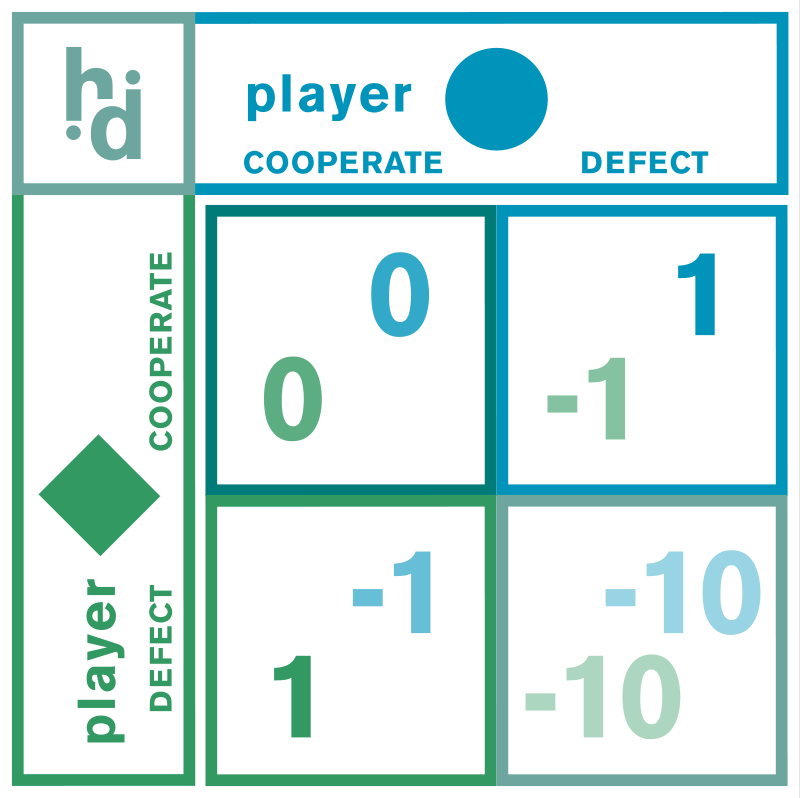
Beispiel: Gefangenendilemma

Zwei Angeklagte werden des gemeinschaftlichen Betruges beschuldigt. Kooperieren die Angeklagten in ihrer gemeinsamwn Verteidigung vor Gericht, etwa indem sie sich gegenseitig ein Alibi liefern, drohen jedem maximal 2 Jahre Haft. Bietet sich ein Angeklagter als geständiger Kronzeuge an, wird dieser freigesprochen, doch dem anderen drohen dann 10 Jahre Haft. Wie sollen sich die Angeklagten verhalten? Das ist kurz behandelt im Artikel zum Gefangenendilemma ↗

Spieltheorie und Evolution

Die klassische Spieltheorie fand unter anderem eine breite Anwendung in den Wirtschaftswissenschaften. Der Engländer John Maynard Smith übertrug die entsprechenden mathematischen Modelle dann auf die biologische Evolution^[2]. Sollen zum Beispiel Geschwister sich gegenseitig helfen oder sich gegenseitig die Ressourcen wegnehmen? Aus Sicht der Evolutionsbiologie (Genegoismus) kann es sich für Geschwister lohnen zu kooperieren, da sie jeweils die hälfte ihrer Gene gleich haben und ein Gedeihendes Bruders oder der Schwester damit auch eigene Gene fördert. Aber auch eine scharfe Konkurrenz kann ein Vorteil sein: schaltet man jede elterliche Fürsorge für ein Geschwisterteil aus, erhält man eventuell mehr als die doppelten Ressourcen wie vorher. Siehe auch Das egoistische Gen [Buch] ↗

Fußnoten

[1] John von Neumann: Neumann: On the Theory of Games of Strategy. In: Tucker, A. W.; Luce, R. D. (eds.). Contributions to the Theory of Games. Vol. 4. pp. 13–42. 1959. ISBN 0-691-07937-4.

[2] John Maynard Smith: Evolution and the theory of games. Cambridge New York: Cambridge University Press. 1982. ISBN 978-0-521-28884-2.

[3] "GAME THEORY: A general theory of rational BEHAVIOR for situations in which (1) two (two-person games) or more (multi-person games) DECISION makers (players) have available to them (2) a finite number of courses of action (plays) each leading to (3) a well defined outcome or end with gains and losses expressed in terms of numerical payoffs associated with each combination of courses of action and for each decision maker. The decision makers have (4) perfect knowledge of the RULEs of the game, i.e., (1), (2) and (3) but no knowldege about the opponents' moves and are (5) rational in the sense of making decisions that optimize their individual gains. The MATRIX of payoffs can represent various CONFLICTs. In a zero-sum game one person wins what the other looses. In other situations gains and losses may be unequally distributed which allows the representation of numerous compfrtitive and conflict situations. The theory proposes several solutions, e.g., in a minimax strategy each participants minimize's the maximum loss the other can impose on him, a mixed strategy involves PROBABILISTIC choices. Experiments with such games revealed conditions for cooperation, defection and the persistence of conflict. The theory and some of the results have found applications in economics, management SCience bargaining and conflict resolution among many areas of interest." In: Klaus Krippendorf: A Dictionary of Cybernetics. Annaberg School of Economics. University of Pennsylvania. 1986. Online: https://asc-cybernetics.org/publications/Krippendorff/A_Dictionary_of_Cybernetics.pdf