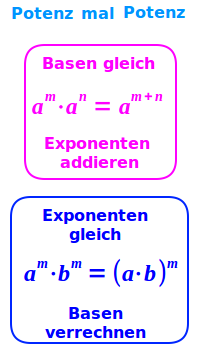
Potenz mal Potenz
Vereinfachen
© 2016
- 2026
Basiswissen
2²·4² oder 5³·5¹ können beide mit leichten Umformungsregeln vereinfacht werden ohne dass man dabei aufwändig rechnen muss. Fachworte und die zwei wichtigsten Fälle sind hier mit Zahlenbeispielen kurz erklärt.
Vorab
- Einen Ausdruck wie 2³ nennt man eine 👉 Potenz
- Die Zahl unten, hier die 2, ist die 👉 Basis
- Die Zahl oben, hier die 3, heißt 👉 Exponent
Basen gleich
- Wie 2³ mal 2²
- Man schreibt die gemeinsame Basis hin, also: 2
- Man addiert die Exponenten, das gäbe hier die 5.
- Diese Summe schreibt man als neuen Exponenten, also 2^5.
- Das wäre ausgerechnet als Zahl: 2·2·2·2·2 was genau 32 gibt.
- Siehe auch 👉 Potenzen mit gleicher Basis multiplizieren
Exponenten gleich
- Wie 4³ mal 0,5³
- Man multipliziert die Basen, das gibt: 2
- Man setzt den gemeinsamen Exponenten darüber: 2³
- Ausgerechnet gäbe das dann 2·2·2, also die Zahl 8.
Nichts ist gleich
- Wie 2^4 mal 3^2
- Man kann nur die Potenzen einzeln ausrechnen ...
- und sie danach multiplizieren. Das gäbe hier:
- 16 mal 9 oder am Ende die Zahl 144.