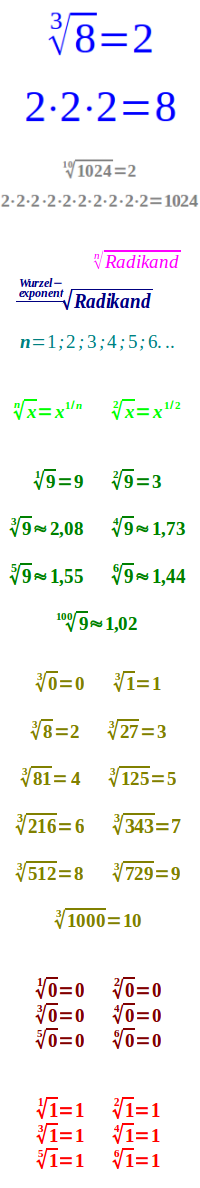Definition

Die n-te Wurzel aus einer Zahl x, ist die Zahl, die n mal in einer Malkette stehen muss, dass x herauskommt.

Bildbeschreibung und Urheberrecht — Man sieht mehrere Wurzeln mit natürlichzahligen Exponenten.☛

Beispiele

Die 1-te Wurzel von 4 wäre 4, weil 4 selbst 4 ist.

Die 2-te Wurzel von 9 ist 3, weil 3·3 wieder 9 gibt.

Die 3-te Wurzel von 64 ist 4, weil 4·4·4 wieder 64 gibt.

Die 4-te Wurzel von 81 ist 3, weil 3·3·3·3 wieder 81 gibt.

n

Das n steht für eine beliebige natürliche Zahl.

Natürlich sind z. B. die 1; 2; 3; 4; 25; 26 und so weiter.

[Die 0 gehört nicht zu den natürlichen Zahlen.]

Sprechweisen

Die "erste Wurzel" von x ist x selbst.

Die zweite Wurzel nennt man auch die Quadratwurzel ↗

Die dritte Wurzel nennt man auch die Kubikwurzel ↗

Die vierte Wurzel nennt man nur die vierte Wurzel ↗

Berechnung

Bei vielen Zahlen nur überschlägig oder mit Taschenrechner.

Bei manchen Zahlen geht es aber auch schnell im Kopf.

Es hilft eine immer gleiche Rechenfrage:

Die dritte Wurzel von 8 "erfragt" man so:

Was muss 3mal in einer Malkette stehen, dass 8 herauskommt?

Verallgemeinerung hin zur r-ten Wurzel

Die n-te Wurzel^[1] einer Zahl z kann man sich anschaulich als diejenige Zahl vorstellen, die n mal als Faktor in einer Malkette stehen muss, dass der Wert der Malkette, das rechnerische Produkt, genau die Zahl z ergibt.^[2] Diese Vorstellung versagt, wenn man nach der 1,5ten Wurzel oder der ½ten Wurzel fragt. Die 1,5te Wurzel von der Zahl 8 etwa müsste dann 1,5 mal in einer Malkette stehen, um die Zahl 8 zu ergeben. Das macht keinen Sinn. Tatsächlich ist die 1,5te Wurzel von der 8 die Zahl 4. Wie man durch eine Verallgemeinerung der Idee der Wurzel dazu kommt, ist erklärt im Artikel über die r-te Wurzel ↗

Diskussion

In manchen Lehrbüchern findet man auch, dass die n-te Wurzel als definiert wird als "diejenige postive Zahl, die n-mal mit sich selbst multipliziert a ergibt."^[7] Ich halte diese Definition für irrefürend. Betrachten wir die dritte Wurzel von 8. Das ist die Zahl 2. Als Malkette geschrieben ist das 2·2·2. Wie oft multipliziert man die zwei hier mit sich selbst? Man hat ja nur zwei Malzeichen. Also gibt es höchstens auch zwei und nicht drei Multiplikationen. Auch verwirren könnte, dass man ja nicht wiederholt die 2 mit sich selbst multipliziert. Drei mal die zwei mit sich selbst multiplizieren könnte man auch deuten als 2·2, dann noch mal 2·2 und dann noch mal 2·2. Auch gilt, dass die Zahl -8 als dritte Wurzel die -2 hat. Die dritte Wurzel darf also durchaus positiv sein. Die für uns klarer Formulierung wäre: die n-te Wurzel aus einer Zahl a ist diejenige Zahl, die drei mal in einer Malkette stehen muss, deren Wert am Ende wieder a gibt.

Fußnoten

[1] Der Ausdruck nte Wurzel ist verwendet in: "Die Berechnung dieser positiven Zahl heißt Ausziehen der nten W. aus a (Radizieren) und erfolgt am raschesten mit Hilfe der Logarithmen (s. Logarithmus), die man außer im Falle n = 2 stets benutzt." In:

Meyers Großes Konversations-Lexikon, Band 20. Leipzig 1909, S. 796-797. Online: http://www.zeno.org/nid/20007709129

[2] "Wurzel, in der Mathematik die Zahl, die man durch Zerlegung einer gegebenen Zahl, des Radikanden, in mehrere gleich große Faktoren erhält; die Anzahl dieser Faktoren heißt der Wurzelexponent, und nach ihr wird die W. benannt." In: Meyers Großes Konversations-Lexikon, Band 20. Leipzig 1909, S. 796-797. Online: http://www.zeno.org/nid/20007709129

[3] Zum Beispiel in: Henning Körner (Herausgeber): Mathematik. Neue Wege 10. Westermann Verlag. Druck aus dem Jahr 2023. ISBN: 978-3-14-125605-5. Dort im Kapitel "1. Potenzen" im Check-up auf Seite 29.