ℜ
Physik Chemie Grundschule Mathematik I Mathematik II Wissen
Kurze Worte Worte nach Alter Terme Rechner
Mathfeed Physfeed Philfeed
Das Lexikon Die Mission Die Autoren Copyright Impressum
Physik 5-10 Physik 11-13 Chemie 5-13 Mathe 5-8 Mathe 9-10 Mathe 10-13
☰
A B C D E F G H I J K L M N O P Q R S T U V W X Y Z 9 Ω
Das Banner der Rhetos-Website: zwei griechische Denker betrachten ein physikalisches Universum um sie herum.

Lineare Abbildung

Graphisch

Basiswissen


Eine lineare Abbildung[1] oder lineare Transformation[2] wird oft in Verbindung mit Veränderungen von 2D- oder 3D-Figuren über Matrizen behandelt. Diese Anwendung wird hier kurz vorgestellt.

Definition einer linearen Abbildung über Vektoren


Das Wort lineare Abbildung wird zunächst mit Hilfe von Vektoren[4] definiert: "Bei einer linearen Abbildung ist es unerheblich, ob man zwei Vektoren zuerst addiert und dann deren Summe abbildet oder zuerst die Vektoren abbildet und dann die Summe der Bilder bildet. Gleiches gilt für die Multiplikation mit einem Skalar aus dem Grundkörper."[1]

Definition einer linearen Abbildung in der Analysis


Was oben für Vektoren definiert wird, kann auch auf Funktionen der Analysis übertragen werden. Die Rolle der Vektoren sind dann die Funktionsargument v₁ und v₂ sowie die dafür möglichen Funktionswerte:


Bei einer linearen Abbildung im Sinne der Analysis ist es unerheblich, ob man zwei Funktionsargumente (v₁ und v₂) zuerst addiert und dann den Funktionswert für deren Summe berechnet oder zuerst die Funktionswerte der zwei Argumente einzeln bildet und die Funktionswerte dann addiert. Gleiches gilt sinngemäß auch für die Multiplikation. Die erste Bedingung bezeichnet man auch als Additivität, die zweite als Homogenität.[3]

Matrizen für lineare Abbildungen


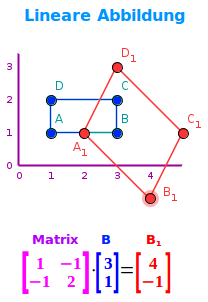
Man stelle sich ein xy-Koordinatensystem vor. In ihm werden vier Punkte definiert: A(1|1), B(3|1), C(3|2) sowie D(1|2). Diese vier Punkte bilden die Ecken eines Rechtecks. Jeder der Punkte kann auch als Ortsvektor gedacht werden. Nun sei eine quadratische Matrix gegeben: (1,1|-1,2). Die ersten zwei Zahlen entsprechen der ersten Zeile, die letzten zwei Zahlen der zweiten Zeile. Nun kann man diese Matrix mit jedem einzelnen der Eckpunkt-Vektoren multiplizieren. Dabei entstehen vier neue Punkte: A'(2|1), B'(4|-1), C'(5|1) sowie D'(3|3). Diese vier neuen Punkte haben das ursprüngliche Rechteck zum einen gedreht und zum anderen in ein schiefes Parallelogramm verwandelt. Es gibt nun bestimmte Matrizentypen, die immer zu bestimmten Typen einer Abbildung oder Transformation gehören. Die folgenden Transformationen sind lineare Abbildung:


Fußnoten




Das blaue Rechteck wird als rotes Parallelogramme abgebildet. Darunter steht die Rechnung beispielhaft für den Punkt B: man multipliziert die Transformationsmatrix mit dem Ortsvektor zu B. Das Ergebnis ist der Ortsvektor zu B'. Gunter Heim