Beispiele
f'(x) noch einmal abgeleitet ergibt die zweite Ableitung f''(x). Dazu stehen hier einige Beispiele. => Ganzen Artikel lesen …
Mathematisch
In dem Wort TAU ist der Buchstabe A der zweite Buchstabe. Und in einer neuen Woche ist der Dienstag der zweite Tag. Der erste Tag ist der Montag. Man spricht von einer sogenannten Ordinal- oder Ordnungszahl. Das ist hier kurz erklärt. => Ganzen Artikel lesen …
 Ableitung
Ableitung
f'(x)
Die Ableitung steht einmal für die Steigung (als Zahl) an einem bestimmten Punkt auf einem Funktionsgraphen. Präziser spricht man hier auch vom Ableitungswert. Als Ableitung bezeichnet man auch eine Funktion f'(x), die für jeden x-Wert die dort geltende Steigung am Graphen angibt.[1][2] Präziser wäre hier: Ableitungsfunktion => Ganzen Artikel lesen …
… siehe unter => Zweite Ableitung bilden
f(x) viermal hintereinander ableiten
Die vierte Ableitung von f(x) = x⁵ ist f''''(x) = 120x. Leitet man eine Funktion viermal hintereinander ab, ist das Ergebnis die sogenannte vierte Ableitung. Dazu steht hier noch ein Beispiel. => Ganzen Artikel lesen …
Anleitung
Man leitet eine Funktion f(x) ab, die Ableitung davon erneut und deren Ableitung wieder. Das Endergebnis ist dann die dritte Ableitung f'''(x). Ausgesprochen wird das als f-drei-Strich-von-x. Das ist hier kurz mit Beispielen vorgestellt. => Ganzen Artikel lesen …
Beispiele
f(x) = x³ einmal abgeleitet gibt f'(x) = 3x². Das dann noch einmal abgleitet gibt f''(x) = 6x¹. Dazu stehen hier noch einige Beispiele. => Ganzen Artikel lesen …
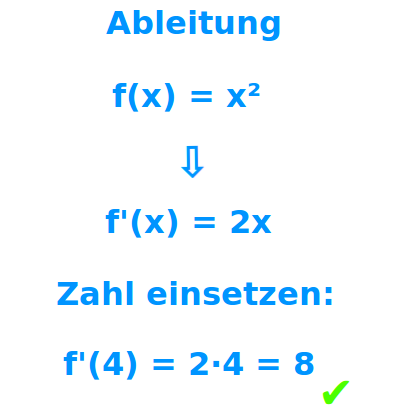
f'(x)
f(x) = x² ⭢ einmal ableiten gibt ⭢ f'(x) = 2x. Das f'(x) ist die erste Ableitung. Sie zu berechnen nennt man oft auch sie zu bilden. Das ist hier kurz vorgestellt. => Ganzen Artikel lesen …

