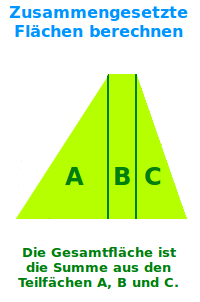
Zusammengesetzte Flächen berechnen
Anleitung
Oft kann man größere Flächen in mehrere kleine Flächen zerlegen. Für die so entstandenen Teilflächen gibt es oft spezielle Formeln mit denen sie (vergleichsweise) leicht berechnet werden können. Die Gesamtfläche ist dann gleich der Summe der Teilflächen. => Ganzen Artikel lesen …
Flächen
Verschiedene Arten (mathematisch)
Eine Fläche in der Mathematik (Geometrie) ist eine Teilmenge eines dreidimensionalen Raumes. Flächen werden üblicherweise als begrenzt (also nicht unendlich ausgedehnt) betrachtet. Sie können flach sein (Rechteckfläche) oder auch gekrümmt (Kugeloberfläche). Normalerweise werden sie als zusammenhängend betrachtet (verstreute Punkte bilden keine Fläche). Hier werden einige Arten kurz vorgestellt. => Ganzen Artikel lesen …
Berechnen
Definition
Bis auf einen Zahlenwert genau bestimmen. Man kann zum Beispiel den Gesamtpreis von 4 Äpfeln berechnen, wenn man weiß, dass jeder einzelne Apfel 50 Cent kostet. Man rechnet: 4 mal 50 Cent und hat als Gesamtpreis dann 200 Cent oder genau 2 €. => Ganzen Artikel lesen …
Zusammengesetzte Fläche
Aus Teilchenflächen gebildet
Eine Fläche nennt man zusammengesetzt, wenn man sie so vorstellt, als sei sie aus meheren kleineren Teilflächen zusammengesetzt worden. Lies mehr dazu unter => zusammengesetzte Flächen berechnen
… ist r*s*Siehe unter => Kegelmantelfläche
… zum Beispiel in cm², siehe unter => Kugelkalottenfläche
Würfel, Quader, Prismen, Zylinder, Kegel
Die Mantelflächen sind anschaulich gesagt die senkrechten oder schräg nach oben gehenden Seitenflächen eines Körpers, wenn er auf der Grundfläche steht. Für verschiedene Körper gibt es angepasst Formeln, auf die hier verwiesen wird. => Ganzen Artikel lesen …
Beispiele
4, 6, 8, 9, 10, 12, 14, 15, 16, 18, 20, 21, 22, 24, 25 sind zusammengesetzte Zahlen. Eine Definition steht unter => zusammengesetzte Zahl
