 Unitäre Matrix
Unitäre Matrix
Definition
Eine unitäre Matrix U, üblicherweise mit einem großen lateinischen U gekennzeichnet, ist auf verschiedene, aber miteinander übereinstimmende Weisen definiert. Hier sind zwei Definitionen kurz vorgestellt. => Ganzen Artikel lesen …
 Matrix
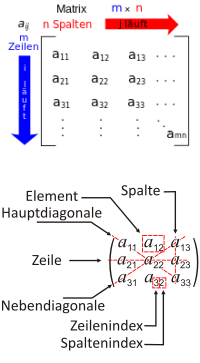
Matrix
Mathematik
Kurzdefinition: eine Matrix ist eine tabellartige Anordnung von Elementen, meist von Zahlen. Mit Matrizen kann man dann verschiedene Rechnungen durchführen [1], so als sei die ganze Matrix eine Zahl. => Ganzen Artikel lesen …
 Inverse Matrix
Inverse Matrix
A⁻¹
Ein inverse Matrix, auch Kehrmatrix, Umkehrmatrix oder kurz Inverse ist eine Art Kehrwert in der Matrizenrechnung. Hat man eine Matrix A, dann gibt das Produkt aus A und ihrer Inversen A⁻¹ immer die sogenannte Einheitsmatrix 𝟙, kurz: A·A⁻¹=𝟙. => Ganzen Artikel lesen …
Determinante ist nicht 0
Der Begriff ist nur für quadratische Matrizen definiert. Eine quadratische Matrix hat genauso viele Spalten wie Zeilen. Eine solche Matrix heißt genau dann regulär, wenn ihre Determinante einen von 0 verschiedenen Wert annimmt. Wie man die Determinante einer Matrix bestimmt steht unter => Determinante berechnen
Matrizen
Determinante ist 0: [1] der Begriff ist nur für quadratische Matrizen definiert. Eine quadratische Matrix hat genauso viele Spalten wie Zeilen. Eine solche Matrix heißt genau dann singulär, seltener auch entartet [2][4], wenn ihre Determinante den Wert 0 annimmt. Nimmt sie einen von Null verschiedenen Wert an, ist sie eine reguläre Matrix. => Ganzen Artikel lesen …
Physik
Man nennt eine Matrix unimodular, wenn all ihre Einträge aus rein ganzzahligen Zahlen bestehen und auch ihre inverse Matrix nur ganzzahlige Einträge enthält. Es dürfen also negative Zahlen und die Null vorkommen, aber zum Beispiel keine echten Kommazahlen. Wenn die Determinante einer Matrix Wert 1 oder den Wert -1 hat, dann ist sie unimodular. => Ganzen Artikel lesen …
Aᴴ
Adjungiert oder auch transponiert-konjugiert nennt man eine Matrix, „die aus einer (n × n)-Matrix A = (aᵢⱼ) über ℝ oder ℂ durch Vertauschen von Zeilen und Spalten und anschließende komplexe Konjugation entstandene (n × n)-Matrix [1]“. Diese Definition ist hier kurz vorgestellt. => Ganzen Artikel lesen …

