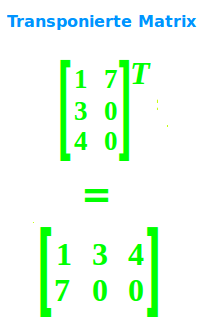Transponierte Matrix
Aᵀ
Eine transponierte [1], gestürzte [2] oder gespiegelte Matrix ist eine Matrix, bei der ausgehend von einer anderen Matrix die Spalten (oben nach unten) zu Zeilen (links nach rechts) gemacht wurden. Das wird hier kurz mit Beispielen erklärt. => Ganzen Artikel lesen …
… die Transponierte meint meist eine => transponierte Matrix
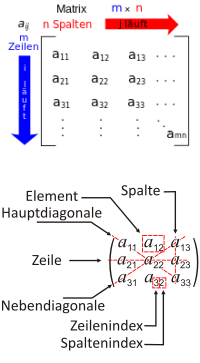
Matrix
Mathematik
Kurzdefinition: eine Matrix ist eine tabellartige Anordnung von Elementen, meist von Zahlen. Mit Matrizen kann man dann verschiedene Rechnungen durchführen [1], so als sei die ganze Matrix eine Zahl. => Ganzen Artikel lesen …
Aᴴ
Adjungiert oder auch transponiert-konjugiert nennt man eine Matrix, „die aus einer (n × n)-Matrix A = (aᵢⱼ) über ℝ oder ℂ durch Vertauschen von Zeilen und Spalten und anschließende komplexe Konjugation entstandene (n × n)-Matrix [1]“. Diese Definition ist hier kurz vorgestellt. => Ganzen Artikel lesen …
Definition
Das Wort konjugierte Matrix bezieht sich nur auf komplexe Matrizen, also Matrizen deren Elemente alle komplexe Zahlen sind. Die konjugierte Matrix aus einer Ausgangsmatrix bildet man dadurch, dass man jedes einzelne Element, also jede einzelne komplexe Zahl, konjugiert. Die komplexe Zahl 4+3i ist konjugiert die Zahl 4-3i. Siehe auch => konjugiert komplexe Zahl
