Sphärischer Kreis
Geometrie
Ein Kreis ganz auf eine Kugeloberfläche gezeichnet: in Anlehnung an ein sogenanntes sphärisches Dreieck [1] kann man auch andere Objekte als sphärisch bezeichnen, die ganz auf einer Kugeloberfläche liegend gedacht sind. Das Besondere bei einem solchen Kreis ist, dass auch der Kreisradius und der Kreisdurchmesser ganz auf der Kugeloberfläche gedacht werden. Das hat einige interessante Konsequenzen, die hier kurz angedeutet sind. => Ganzen Artikel lesen …
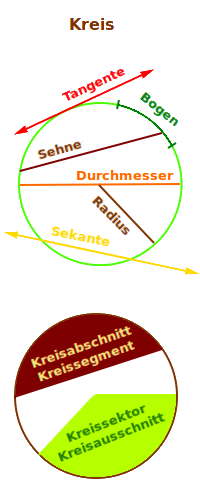
Kreis
◯ Definition und Übersicht
Ein Kreis ist ist die Menge aller Punkte, die gleich weit von ihrem gemeinsamen Mittelpunkt entfernt sind. Der Kreis spielt in der Geometrie eine große Rolle. Hier sind die wichtigsten Fachworte und Formeln zusammengestellt. => Ganzen Artikel lesen …
Sphärisches Dreieck
Anschaulich
Ein Dreieck auf eine Kugeloberfläche gezeichnet: wählt man drei verschiedene Punkte auf einer Kugeloberfläche aus, dann kann man diese durch möglichst kurze Linien auf der Kugeloberfläche verbinden. Das so entstandene Dreieck nennt man ein sphärisches Dreieck oder auch Kugeldreieck. Das dazugehörige Gebiet der Mathematik ist die sphärische Geometrie. Das ist hier kurz vorgestellt. => Ganzen Artikel lesen …
… in der Wirtschaft, siehe unter => Preiselastizität
… meint am ehesten eine => Ellipse
Sphärische Linse
Kugelförmig
Sphärisch (kugelartig) nennt man optische Linsen die mindestens eine optisch wirksame Oberfläche haben, die von der Form her Teil einer Kugeloberfläche ist. Bei einer klassischen Sammellinse können beide Seiten kugelartig nach außen gewölbt sein (konvex-konvex). Häufig anzutreffen sind aber auch sphärische Linsen, bei denen nur eine Seite sphärisch ist, die andere hingegen eben oder plan ist (plan-konvex). => Ganzen Artikel lesen …
Definition
Eine asphärische Linse ist eine Linse, mit mindestens einer brechenden Oberfläche, die nicht sphärisch und nicht plan (flach) ist. Mit passend geformten solchen Linsen lassen sich Abbildungsfehler, wie etwa die sphärische Aberration, vollständig korrigieren. => Ganzen Artikel lesen …
