Anschaulich
∂f/∂x und ∂z/∂x: der Graph einer Funktion mit zwei unabhängigen Variablen kann oft als Ebene im dreidimensionalen Raum dargestellt werden. Die partiellen Ableitungen ∂f/∂x und ∂z/∂x geben dann die Steigung in die Richtung parallel zu je einer der Koordinatenachsen der jeweils im Nenner angegebenen unabhängigen Variablen x oder y an. Das ist hier kurz vorgestellt. => Ganzen Artikel lesen …
 Ableitung
Ableitung
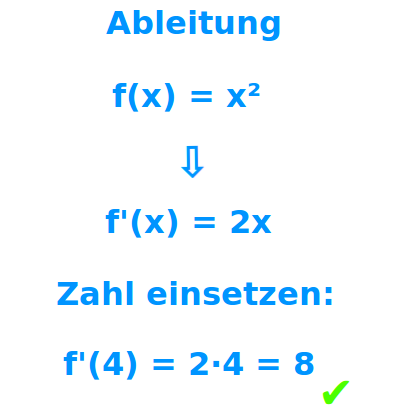
f'(x)
Die Ableitung steht einmal für die Steigung (als Zahl) an einem bestimmten Punkt auf einem Funktionsgraphen. Präziser spricht man hier auch vom Ableitungswert. Als Ableitung bezeichnet man auch eine Funktion f'(x), die für jeden x-Wert die dort geltende Steigung am Graphen angibt.[1][2] Präziser wäre hier: Ableitungsfunktion => Ganzen Artikel lesen …
… Erklärung mit Beispiel unter => Partiell integrieren
Anleitung wie es geht
Höhere Mathematik: partiell ableiten heißt, dass man für eine Funktion mit zwei unabhängigen Variablen x und y die Ableitung entweder für x oder für y bildet. => Ganzen Artikel lesen …
… eine Funktion mit x und y, siehe unter => partiell ableiten
… eine Funktion mit x und y, siehe unter => partiell ableiten

