Vektoren
Zwei Vektoren sind zueinander orthonormal, wenn sie sowohl senkrecht aufeinander stehen, also das Skalarprodukt haben sowie zusätzlich auch beide noch die Länge (Betrag) Eins haben. Siehe auch => orthogonal
⊗☉↗⮅ Arten und Einteilung
Vektoren sind gedachte Pfeile in einem 2D-, 3D- oder höherem Koordinatensystem. Sie werden oft aus zwei oder drei Zahlen zusammengesetzt, etwa (4|3|5). => Ganzen Artikel lesen …
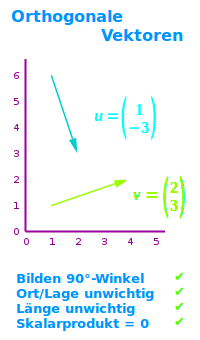Orthogonale Vektoren
90°-Winkel
Orthogonale Vektoren sind hier zwei oder mehr Vektoren, die zueinander orthogonal, das heißt rechtwinklich sind, also einen 90°-Winkel einschließen. Das Skalarprodukt solcher zueinander orthogonaler Vektoren ist immer 0. => Ganzen Artikel lesen …
Bedeutungen
Man unterscheidet einen Normalenvektor und einen normierten Vektor. Erster steht mit 90° auf etwas anderem, der zweite hat die Länge 1. Beides ist hier kurz behandelt. => Ganzen Artikel lesen …
n₀
Jeder Vektor, der in einem 90°-Winkel auf einer Ebene steht, ist ein Normalenvektor dieser Ebene. Jeder Vektor, der in einem 90°-Winkel zu einer Geraden steht, ist ein Normalenvektor dieser Geraden. Normal heißt hier soviel wie „senkrecht auf“, also dasselbe wie orthogonal oder im 90°-Grad Winkel: ein Normalenvektor, auch Lotvektor genannt und oft abgekürzt als n₀, steht immer senkrecht auf etwas anderem. Normalenvektoren treten insbesondere bei der Definition von Ebenen im dreidimensionalen Raum ℝ³ auf. => Ganzen Artikel lesen …
