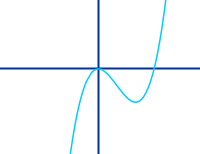
Nicht achsensymmetrisch
Übersicht
Ein Graph oder auch ein 2D- oder 3D-Gebilde kann keinerlei Symmetrieachse haben, ist dann also auch nicht achsensymmetrisch. Hier werden drei häufige Fälle kurz vorgestellt. => Ganzen Artikel lesen …
Nicht
Mathematik
Nicht-rund, nicht-künstlich oder nicht-flach: das Wort Nicht steht in der Mathematik meist für die Idee einer direkten Verneinung, also das logische Gegenteil. Mehr zur Idee des logischen Gegenteils unter => logisches Nicht
Achsensymmetrisch
Mathematisch
Achsensymmetrisch, heißt, dass etwas eine Mittellinie hat und links und rechts davon sieht die Figur gleich aus. Mathematisch: es gibt mindestens eine Symmetrieachse. Lies mehr dazu unter => Achsensymmetrie
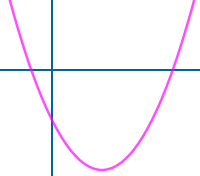Nicht punktsymmetrisch
Übersich
Es gibt keinen Symmetriepunkt oder - im engeren Sinn von Funktionsgraphen - der Punkt (0|0) ist kein Symmetriezentrum des Graphen. Die Fälle sind hier kurz vorgestellt. => Ganzen Artikel lesen …
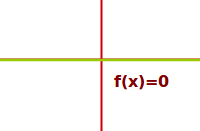Punktachsensymmetrie
Beispiel
Sowohl punkt- als gleichzeitig auch achsensymmetrisch: ein Funktionsgraph, der sowohl Punktsymmetrisch zum Koordinatenursprung als auch achsensymmetrisch zur y-Achse ist der Graph von f(x)=0, also die => Nullfunktion
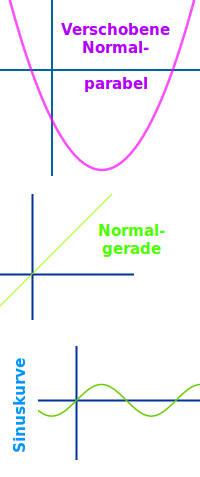Nicht achsensymmetrisch zur y-Achse
Beispiele
Eine verschobene Normalparabel, die Sinuskurve, der Graph von f(x)=x³ oder die Normalgerade: wenn die y-Achse nicht die Symmetrieachse ist, dann sind die Graphen auch nicht achsensymmetrisch zur y-Achse. Mehr unter => Achsensymmetrie von Graphen
