 Nach oben geöffnet
Nach oben geöffnet
Parabel
Die Graphen von ganzrationalen Funktionen nennt man Parabeln. Solche Parabeln haben immer einen linken und einen rechten Ast. Gehen beide Äste vom Scheitelpunkt aus nach oben, dann sagt man: die Parabel ist nach oben geöffnet. Das ist hier kurz vorgestellt. => Ganzen Artikel lesen …
Lagewort
In dem Namen „Kasper“ steht der Buchstabe s nach dem Buchstaben a. Auch das p kommt erst nach dem a. Nach heißt so viel wie dahinter oder später. Eine Zahl, die direkt nach einer anderen Zahl kommt nennt man in der Mathematik einen => Nachfolger
Physik
Unten im Tal und oben auf dem Gipfel des Berges: den meisten Menschen scheint zunächst klar zu sein, was unten und oben bedeutet. Im fünften Stock eines fünfstöckigen Hauses ist man oben, im Erdgeschoss oder im Keller ist man unten. Doch blickt man vom Weltraum auf die Erde, dann ist es auf einmal nicht mehr so klar, was oben und unten heißen soll. Das ist hier kurz vorgestellt. => Ganzen Artikel lesen …
 Nach unten geöffnet
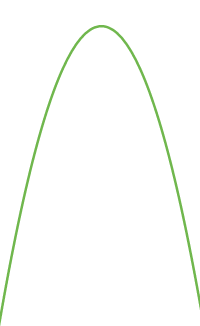
Nach unten geöffnet
Parabel
Die Graphen von ganzrationalen Funktionen nennt man Parabeln. Parabeln haben immer einen linken und einen rechten Ast. Gehen beide Äste vom Scheitelpunkt aus nach unten, dann sagt man: die Parabel ist nach unten geöffnet. Das ist hier kurz vorgestellt. => Ganzen Artikel lesen …
 Nach links geöffnet
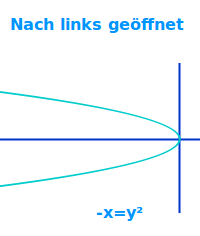
Nach links geöffnet
Parabel
-x=y²: dies ist die Gleichung einer querliegenden Parabel, deren Scheitelpunkt rechts im Koordinatensystem liegt und deren zwei Äste von dort aus nach links gehen. Der Graph gehört zu einer Zuordnung, aber nicht zu einer Funktion. Das ist hier näher erklärt. => Ganzen Artikel lesen …
… Definition und Formeln unter => senkrechter Wurf
 Nach oben geöffnete Parabel
Nach oben geöffnete Parabel
Wie normale U
Der Scheitelpunkt ist der tiefste Punkt einer nach oben geöffneten Parabel. Die beiden Parabeläste zeigen nach oben. Lies mehr dazu unter => nach oben geöffnet
… der Graph von f(x)=x², heißt offiziell einfach nur => Normalparabel

